72. Soluzioni del 5 dicembre 2022 – In Olanda con Pythagoras Magazine

Soluzioni del 5 dicembre 2022 a cura di Fabio Ciuffoli

Ieri abbiamo proposto tre giochi che sono stati pubblicati su un’edizione speciale di Pythagoras Magazine, la rivista di matematica ricreativa più famosa dei Paesi Bassi e di seguito presentiamo le nostre soluzioni. 

In Olanda con Pythagoras Magazine – soluzioni

1. In una borsa ci sono 26 banconote. Se estrai 20 banconote a caso dalla borsa, hai almeno una banconota da 1 dollaro, due banconote da 2 dollari e cinque banconote da 5 dollari. Quanti dollari, in totale, c’erano nella borsa?

1. SOLUZIONI. Definiamo A il numero di banconote da 1 dollaro nella borsa, B il numero di banconote da 2 dollari e infine C il numero di banconote da 5 dollari. Sappiamo che se si tolgono 20 banconote ne rimangono 6, quindi:

• A ≥ 6 + 1 = 7
• B ≥ 6 + 2 = 8
• C ≥ 6 + 5 = 11

quindi A + B + C ≥ 26 e poiché nella borsa ci sono 26 banconote, A + B + C = 26, e quindi A = 7, B = 8 e C = 11. Il valore totale è (7 * 1) + (8 * 2) + (11 * 5) = 78 dollari.

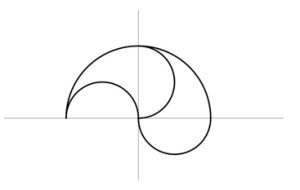
2. Il simbolo Yin-Yang, nella figura sotto, è delimitato da tre semicerchi. Come si può dividere questa figura in due forme identiche?

2. SOLUZIONE. Abbiamo aggiunto le linee della griglia per mostrare esattamente dove deve andare il taglio semicircolare.

3. Una torta enorme è divisa tra 100 ospiti. Il primo ospite riceve l’1% della torta. Il secondo ospite riceve il 2% della parte rimanente. Il terzo ospite riceve il 3% del resto, ecc. L’ultimo ospite ottiene il 100% dell’ultima parte. Chi ottiene il pezzo più grande?

3. SOLUZIONE. Quando è il turno dell’ospite numero k, rimane una certa parte, x, della torta. L’ospite k ottiene x moltiplicato per (k/100). E la quantità di torta rimasta sarà: x – x(k/100) = x (100–k)/100. 

Quando arriva il turno del prossimo ospite, che è l’ospite k + 1, otterrà x moltiplicato per [(100–k)/100](k + 1)/100). Pertanto l’ospite k + 1 ottiene più dell’ospite k se [(100–k)/100](k + 1)/100) > k/100. Svolgendo – k² – k + 100 > 0, che è verificata per k = 1, 2, 3, 4, 5, 6, 7, 8 o 9. In altri termini, la quantità di torta presa da ogni ospite continua a crescere fino all’ospite k + 1, nel nostro caso 9 + 1 = 10, quindi il decimo ospite otterrà la fetta più grande e dall’undicesimo ospite le fette di torta saranno più piccole. Possiamo quindi concludere che l’ospite numero 10 ottiene il pezzo più grande. In tabella riportiamo i calcoli e i valori per i primi tredici ospiti.