
I Giochi del Lunedì di Prisma del 3 ottobre 2022 a cura di Fabio Ciuffoli
Oggi presentiamo cinque giochi di natura geometrica, con una particolare cura nella grafica e dotati di una certa armonia e musicalità. Alcuni richiedono qualche calcolo, mentre altri si risolvono solo con l’insight. Invitiamo i lettori a proporre soluzioni e osservazioni nello spazio riservato ai commenti. Domani pomeriggio alle ore 17.00 pubblicheremo le soluzioni argomentate.
Ragnatele, scudi e aree colorate
1. Esagono Ragnatela. Qual è il rapporto tra l’area gialla e l’area celeste? E qual è la somma delle lunghezze di tutti i tratti disegnati in nero?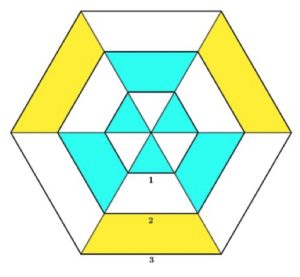
2. Trapezio colorato. Due cateti di un triangolo rettangolo isoscele misurano 50 cm ciascuno e sono stati divisi in 5 parti uguali. Determinare l’area della parte colorata.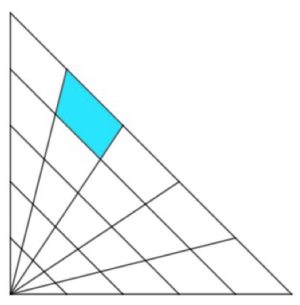
3. Quattro triangoli. Trovare l’area di uno dei quattro triangoli rettangoli uguali.
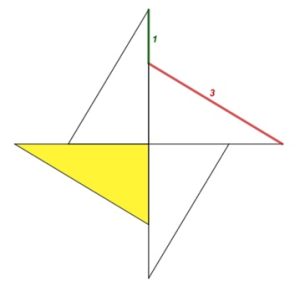
4. Scudo-elica. Ogni quadretto ha per lato 1 cm. Determinare l’area della parte colorata.

5. Area colorata. Determinare l’area verde.
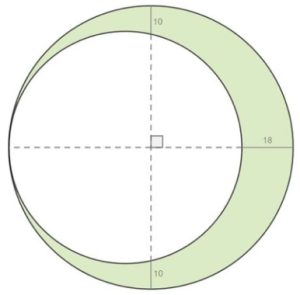
Aggiornamento per le soluzioni click qui.
I giochi sono stati proposti da Roberto Molinelli, stimato musicista, compositore e direttore d’orchestra, in un gruppo social web di divulgazione matematica.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
25 risposte
1 Il rapporto è 1,25
3 L’area è 1,875
5 2500 – 1681 = 819pi greco
Bene 1 e 5. Oggi pomeriggio le soluzioni.
I quattro triangoli. Problema proposto a mia figlia e amiche qualche anno fa con triangoli di cartoncino: capirono subito che la figura andava resa più “gestibile” e calcolarono altrettanto in fretta la soluzione, nella storia dei miei rapporti con Margherita resta un successo.
Problema 2. Il triangolo grande ha area A = 50²/2
Il triangolo che sta sopra all’ultima fetta ha area a = 40²/2
Quindi l’ultima fetta ha area A – a = 50²/2 – 40²/2 = (2500-1600)/2 = 900/2 = 450 cm²
Ora i trapezi alla base avendo tutti le stesse basi maggiori e minori e le stesse altezze hanno tutti la stessa area quindi ciascuno ha area 1/5 della fetta alla base
T = (A – a)/5 = 450/5 = 90 cm²
Soluzione del problema 5, vedi allegato.
Soluzione al problema 4, vedi allegato.
Soluzione al problema 1, vedi allegato
Soluzione al problema 2, vedi allegato con la seguente correzione: c’è un errore di distrazione nel calcolo dell’area ,FG=8rad2 e non 20rad2,così (8rad2+10rad2)×5rad2/2=90.
Problema 2. E’ un trapezio i cui lati paralleli misurano 10*rad2 e 8*rad2; la distanza fra i lati paralleli (altezza) vale 5*rad2. Area: ((10+8)*rad2*5*rad2):2= 18*5*2:2= 90.
1) Prendendo come unità di misura il triangolino equilatero (1/6 dell’esagono centrale):
triangoli azzurri: 3 + 3×3 = 12.
Triangolini, congruenti, gialli: 5×3 = 15. Rapporto aree gialla/azzurra = 15/12 = 5/4.
Lunghezza segmenti neri: 3*6 + 2*6 + 1*6 + 3*6 = 54.
2) Base maggiore 10√2. Base minore 8√2, altezza (50/√2)/5. A = 90 cm^2.
3) Faccio scivolare le ipotenuse lungo i cateti maggiori fino a formare un rombo di lato L = 3, diagonali d2 e d2-1. Con Pitagora, sulle mezze diagonali: [(d2-1)/2]^2 + (d1/2)^2 = 9.
Risolvo l’equazione di 2° grado e trovo d2 = 4.713… Sottraggo 1 e trovo d1.
Moltiplico d1xd2 e divido per 8, ottengo A triangolo = 2.19.
Non mi piace però: troppi calcoli, approssimazioni, secondo me ho sbagliato qualcosa.
4) Le teste dei biscioloni (semicerchi di raggio 1/2) vengono “riempite” dai semicerchi azzurri con un punto in comune. I 4 semicerchi bianchi di raggio r = 1 sono equivalenti al semicerchio di raggio 2.
Resta l’area del rettangolo: 2 x 4 = 8 cm^2.
5) Per ora passo…
1, 2 e 4 soluzioni perfette. La 3 da rivedere, a domani per le soluzioni con dimostrazione
Problema 5. Con Euclide ho (R-10)^2=R*(R-18), da cui R=50. Perciò r=41. L’area verde allora è pigreco*(50^2-41^2)=2.571,66
Problema 5. 819pi come da allegato
N. 2. La striscia dei 5 trapezi più grandi (quelli lungo l’ipotenusa) ha un’area equivalente ai 9/25 dell’intero triangolo rettangolo (perché, escludendo questa striscia, il restante triangolo rettangolo ha i lati lunghi 4/5 del totale, e perciò un’area di (4/5)², ossia 16/25).
Inoltre i 5 trapezi hanno la stessa area, ammettendo che i cinque angoli in cui è diviso l’angolo retto siano uguali, tutti di 18° – anche se questo dato non è presente nell’enunciato del problema -).
Ciascuno perciò ha un’area di 9/125 di quella totale, che è di 1250 cm²
1250 x 9/125 = 90 cm²
Soluzione del problema 3, vedi allegato
3. Trascinare il cateto minore sul cateto maggiore dei triangoli adiacenti fino a formare un quadrato di lato 3 con un “buco” quadrato di area 1.
L’area di questa figura è 3*3-1 e corrisponde all’area dei 4 rettangoli la cui area singola è quindi 2.
1) 1,25
Ottimo. A domani per le soluzioni.
5) 819 pigreco
Perfetto. A domani per le soluzioni.
Problema 1. {[50*50/2]/5}[1-(4/5)^2]=250-16*10=90
N. 3. Detto x il cateto minore: th di Pitagora: 2x^2+2x=8, da cui x^2+x=4, ma x^2+x=x(x+1) cioè il doppio dell’area del triangolo. Quindi 2.
Risposta al 3. (3^2-1)/4 = 2.
Problema n. 3. Area di un triangolo = 2
Problema 4. Ogni virgola bianca è equivalente ad una semicirconferenza di raggio 1. La figura nel complesso è formata da un rettangolo 2×4 e da una semicirconferenza di raggio 2. Pertanto l’area cercata vale
2*4+1/2*pi*4-4*1/2*pi=8