97. Soluzioni del 12 giugno 2023 – La coperta di Fatima e la collana di Aruna

Le soluzioni del 12 giugno 2023 a cura di Fabio Ciuffoli

Ieri abbiamo presentato due problemi che hanno fatto parte del test di ingresso per l’Università di Cambridge e di seguito proponiamo le nostre soluzioni. 

La coperta di Fatima e la collana di Aruna – soluzioni  

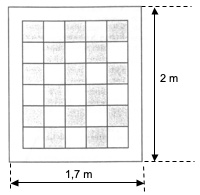1. Fatima sta realizzando una trapunta di dimensioni totali 1,7 metri per 2 metri. Avrà un motivo di 6 x 5 quadrati al centro ed un bordo uguale tutto intorno.Il disegno non è in scala

Di quale dimensione devono essere i quadrati?

1. SOLUZIONE. Si può ragionare intuitivamente oppure utilizzando un sistema di due equazioni con due incognite. Intuitivamente, se il bordo circostante è lo stesso ed in verticale c’è un quadrato in più rispetto all’orizzontale, la differenza tra le due dimensioni dei lati della trapunta (2 – 1,7 = 0,3) deve essere identica al lato di un quadrato. Di conseguenze, ad esempio nella dimensione orizzontale, il bordo sarà: [1,7 – (5 * 0,3)] / 2 = 0,1 m.

Con il sistema, indicando con x la dimensione del lato dei quadrati ed y la distanza dal bordo avremo:

5x + 2y = 1,7   → 2y = 1,7 – 5x             = = =         → 2y = 1,7 – 5 * 0,3       → y = 0,1

6x + 2y = 2      → 6x + 1,7 – 5x = 2     → x = 0,3

La dimensione dei quadrati è 0,3 m x 0,3 m ed il bordo è 0,1 m.

2. La collana di Aruna si è spezzata in due parti perdendo l’anello rotto. La collana è fatta di metallo spesso 2 mm e ciascuno dei due pezzi ha un accessorio all’estremità utilizzato per chiudere la collana, che aggiunge 1 cm alla lunghezza totale. Uno dei due pezzi della collana è lungo 34,2 cm e ha 10 anelli in più dell’altro pezzo, che misura 26,2 cm. Aruna decide di fare ricomporre la collana da un gioielliere, che aprirà e poi chiuderà un anello. Quanti anelli formeranno la collana completa?

2. SOLUZIONE. La collana sarà formata da 72 anelli. La differenza tra i due pezzi è 8 cm e corrisponde alla lunghezza di 10 anelli.

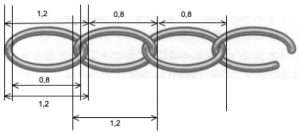
Questo significa che ogni anello ha una lunghezza esterna di 1,2 cm ed interna di 0,8 cm. Solo in questo modo 8 cm corrispondono a 10 anelli.

Dal disegno si individua una progressione: la lunghezza del primo anello è 1,2 cm, la lunghezza di due anelli incatenati è 2 cm, di tre anelli incatenati è di 2,8 cm e via di seguito con un aumento di 0,8 per ogni anello in più.

Nella parte lunga 34,2 cm della collana vi è 1 cm di accessorio alla fine quindi gli anelli sono lunghi 33,2 cm. Questa lunghezza è data da 1 anello di lunghezza intera (1,2 cm) e ed una serie di anelli di lunghezza effettiva di 0,8 cm ciascuno. Per cui il numero di anelli è

1 + [(33,2 – 1,2) / 0,8] = 41.

Il numero 1 davanti alla frazione rappresenta l’anello iniziale che da origine alla progressione 1,2 + 0,8 + 0,8 + 0,8 + …

Lo stesso ragionamento si può fare per la parte più corta della collana

1 + [(25,2 – 1,2)] / 0,8 = 31.

Per cui il numero totale è 41 + 31 = 72.

Segnalo il procedimento di Giorgio Vecchi e di Americo Speranza che riporto di seguito e ringrazio per la collaborazione. 

l = lunghezza totale di un anello; n = numero di anelli del primo pezzo di catena; 2 anelli si sovrappongono per 4 millimetri.
l*n – 4*(n-1) + 10 = 342
l*(n-10) – 4*(n-11) + 10 = 262
si ricava:
l = 12
n = 41
quindi la catena completa avrà 72 anelli e sarà lunga 60cm.

A lunedì prossimo.