Menu
La soluzione del 5 giugno 2023 a cura di Fabio Ciuffoli
Ieri abbiamo presentato un gioco sulle strategie di comunicazione con due studenti alle prese con un esame universitario e di seguito pubblichiamo la nostra proposta di soluzione.
L’esame di Comunicazione – soluzione
Piero e Aldo, due studenti che devono sostenere l’esame di Comunicazione, vengono condotti, uno dopo l’altro, in una stanza dove ci sono quattro scatole vuote identiche numerate: 1, 2, 3 e 4.
Piero entra nella stanza per primo e qui l’insegnante mette un foglio di carta all’interno di una scatola scelta a caso e la richiude. Piero vede in quale scatola si trova il foglio. A questo punto l’insegnante lancia una moneta e la posiziona sulla scatola 1, lancia una seconda moneta e la posiziona sulla scatola 2 e via di seguito per le scatole 3 e 4, come disegnato in figura. Ogni moneta ha una probabilità del 50% di presentare Testa o Croce. Piero può vedere le facce di tutte le monete.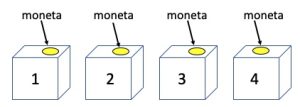
Ora l’insegnante chiede a Piero di scegliere una moneta e girarla in modo che Testa diventi Croce o viceversa. A questo punto Piero andrà in un’altra stanza isolata.
Infine Aldo viene portato nella stanza con le quattro scatole e vedendo le facce delle monete, dovrà aprire una scatola e se la scatola conterrà il foglio di carta, entrambi gli studenti saranno promossi.
Quale strategia garantisce il superamento dell’esame?
Questo è un enigma fantastico perché sembra impossibile che Piero possa comunicare a Aldo, girando una moneta, quale scatola contenga l’anello, in quanto deve considerare le 4 monete e le 16 possibili combinazioni di Testa e Croce. Come vedremo la soluzione sarà sorprendente!
Un suggerimento. Per facilitare la soluzione, ipotizziamo che ci siano solo due scatole. L’insegnante mette il foglio di carta in una delle due scatole e posiziona una moneta a caso su ciascuna scatola. Piero sa quale scatola contiene il foglio e può vedere entrambe le monete.
Quale moneta girerà Piero per comunicare a Aldo il numero della scatola dove si trova il foglio di carta?
SOLUZIONE. Iniziamo risolvendo il caso semplificato con solo due scatole. La soluzione è relativamente semplice: gli studenti decidono che una scatola assumerà il ruolo di “indicatore”, ossia la moneta su di essa indicherà dove si trova il foglio di carta. Supponiamo che scelgano la scatola 1, come “indicatore”, con la regola che se la moneta sulla scatola 1 è Testa, il foglio è nella scatola 1, mentre se la moneta sulla scatola 1 è Croce, il foglio è nella scatola 2. Quindi se Piero vede l’insegnante mettere il foglio nella scatola 2, deve assicurarsi che la moneta sulla scatola 1 mostri Croce, perciò se la moneta sulla scatola 1 è Testa, la gira, mentre se è Croce, gira la moneta sulla scatola 2. Lo stato della moneta sulla scatola 2 è irrilevante per l’identificazione della scatola con il foglio di carta.
Per la soluzione al problema con quattro scatole si utilizza la stessa idea. Tre scatole, supponiamo 1, 2 e 3, costituiranno “l’indicatore” e come sopra, la moneta sulla scatola 4 viene girata solo se le monete su 1, 2 e 3 indicano la casella corretta.
Analizziamo il nostro “indicatore” a tre caselle. Ci sono otto possibili combinazioni delle monete su queste scatole: TTT, CCC, TTC, CCT, TCT, CTC, CTT e TCC.
Sembra incredibile ma esiste un metodo per abbinare queste combinazioni a ogni scatola in modo che, qualunque sia la combinazione iniziale di monete, si possa indicare una delle quattro scatole, girando una sola moneta.
Ecco la strategia che gli studenti devono concordare. Se le prime tre scatole presentano:
In altri termini, se Aldo vede le prime tre scatole con TTT o CCC, significa che il foglio è nella scatola 1, se vede TTC o CCT il foglio è nella scatola 2 e così via.
Supponiamo che Piero voglia indicare la scatola 2 e quando arriva nella stanza trovi la combinazione TCT (che indicherebbe la scatola 3) allora dovrà girare la prima moneta, per ottenere CCT, che come concordato indica la scatola 2. Se osserviamo attentamente tutte le combinazioni, vedremo che si può passare da una combinazione a un’altra, girando una sola moneta. Il procedimento si può illustrare mediante il seguente diagramma.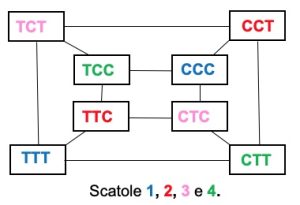 
Il blu indica la scatola 1, il rosso la scatola 2, il rosa la scatola 3 e il verde la scatola 4. Le combinazioni sono collegate ad altre combinazioni che prevedono il cambio di una sola moneta e ogni combinazione è collegata ad altre tre combinazioni di un colore diverso. Nel diagramma qualunque combinazione può essere cambiata per indicare un’altra scatola girando una singola moneta. Ora come deve comportarsi Piero se vedesse una combinazione che sta indicando la scatola corretta? Facile! Gira la moneta sulla casella 4, proprio come nell’ ipotesi semplificata delle due scatole, abbiamo bisogno di una scatola “ridondanza” la cui posizione non ha alcuna attinenza con “l’indicatore”.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
4 risposte
Come avrete notato, ci sono diversi metodi per arrivare alla soluzione. Alcuni più immediati, che si prestano anche a una illustrazione grafica facilmente comprensibile, altri più complessi che portano a una formulazione generale della soluzione. Noi ci siamo attenuti al metodo proposto dell’autore. Rileviamo con piacere che il problema ha suscitato un vivace confronto tra diversi tipi di approccio con ottimi risultati sia di analisi che di sintesi. Un buon lavoro di intelligenza collettiva per il quale ringraziamo i nostri partecipanti collaboratori.
Avevo risolto il problema con due scatole e pensavo di passare a tre, prima di arrivare a quattro. Ma a tre mi sono bloccato. Ho come l’impressione che il gioco, molto bello, sia risolubile solo in alcuni casi
Ma è vero che per tre scatole non c’è soluzione? E, in generale, ci sono altri casi, oltre a 2 e 4 scatole, in cui la soluzione si può trovare?
La soluzione da me prospettata (vedi commento Paci) è più immediata e, oserei dire, più elegante.
La tua risposta è sbagliata, l’autore (identica alla mia) sono quelle al tempo stesso giuste e più ottimizzate.