95. Soluzioni del 29 maggio 2023 – Battaglie matematiche

La soluzioni del 29 maggio 2023 a cura di Fabio Ciuffoli 

Ieri abbiamo proposto tre problemi, che hanno fatto parte di alcune “battaglie matematiche” tra studenti di scuola secondaria organizzate dall’University College di Londra e di seguito presentiamo le nostre proposte di soluzione. 

Battaglie matematiche – soluzioni 

1. Taglio quadrato. Un rettangolo 10 x 12 disegnato su una carta a quadretti viene piegato più volte lungo le linee per ottenere un quadrato 1 x 1. Se tagliassimo questo quadrato a metà lungo una linea parallela a due lati, come illustrato di seguito, quanti fogli di carta separati otterremmo?

E se il quadrato fosse tagliato in diagonale, dal centro del lato sinistro al centro del lato inferiore, quanti pezzi di carta separati otterremmo?

1. SOLUZIONE. Immaginiamo che il quadrato ottenuto sia quello rosso e il taglio (blu) sia dall’alto al basso, come in figura. In questo caso otterremmo 13 pezzi di carta separati. Se il quadrato rosso venisse tagliato orizzontalmente, otterremmo 11 pezzi.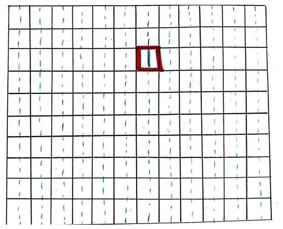   

Nel caso del taglio diagonale dal centro del lato sinistro al centro del lato inferiore, otterremmo 37 pezzi. A seconda del taglio diagonale, con riferimento ai punti cardinali: NE, ES, SO, ON, otterremmo rispettivamente 31, 36, 37 o 43 pezzi di carta separata.

2. Sei lucchetti. Ci sono sei valigie chiuse e sei chiavi, ma non si sa quale chiave sia per quale valigia. Qual è il numero di tentativi di apertura delle valigie necessario per abbinare ciascuna chiave alla rispettiva valigia?

2. SOLUZIONE. Prendiamo la prima chiave e proviamo ad aprire cinque valigie. Se una valigia si aprisse sarebbe un ottimo risultato, tuttavia, se la chiave non aprisse nessuna delle prime cinque valigie, significherebbe che è quella giusta per la sesta valigia.  Possiamo mettere da parte la sesta valigia con la sua chiave. Ora prendiamo un’altra chiave e proviamo ad aprire ognuna delle restanti cinque valigie a turno. Saranno necessari quattro tentativi per determinare a quale valigia appartiene questa chiave. Ripetiamo l’operazione con le restanti quattro valigie e così via. In totale avremo bisogno di 5 + 4 + 3 + 2 + 1 = 15 tentativi.

Generalizzando il numero di valigie e il numero massimo di tentativi, avremo:  per 2 valigie 1 tentativo; per 3 valigie 3 tentativi;  per 4 valigie 6 tentativi; per 5 valigie 10 tentativi; per 6 valigie 15 tentativi. 
La formula generale, indicando con n il numero massimo di tentativi è:  n(n-1)/2

3. Sabotaggio del cubo. Kathy ha otto cubi gialli 1 x 1 x 1 identici. Vuole comporre un cubo 2 x 2 x 2 completamente giallo all’esterno. Peter vuole dipingere di viola alcune delle facce dei cubi 1 x 1 x 1. Qual è il numero minimo di facce che deve dipingere per evitare che Kathy riesca a rendere il suo cubo 2 x 2 x 2 completamente giallo all’esterno?

E cosa succede se Kathy ha 27 cubi 1 x 1 x 1 identici. Quante facce deve dipingere Peter per impedirle di creare un cubo 3 x 3 x 3 completamente giallo all’esterno?

3. SOLUZIONE. Peter deve dipingere solo due facce opposte di un cubo 1 x 1 x 1. Se le facce opposte sono entrambe viola, allora una faccia del cubo 2 x 2 x 2 avrà una parte viola. Nel caso dei 27 cubi, Peter ha bisogno di dipingere due cubi interi, ovvero 12 facce. Se dipingesse solo 11 facce, ci sarebbe sempre un modo per Kathy di nascondere le facce dipinte.

A lunedì prossimo.