94. Soluzioni del 22 maggio 2023 – Dedicato a Ivan Moscovich

Soluzioni del 22 maggio 2023 a cura di Fabio Ciuffoli 

Ieri abbiamo presentato cinque problemi dedicati a Ivan Moscovich, una leggenda nel mondo dei giochi logici e matematici, che ci ha lasciato a fine aprile 2023 all’età di 96 anni. Di seguito pubblichiamo le soluzioni. 

  Dedicato a Ivan Moscovich – soluzioni 

1. Immaginate un filo lunghissimo sul quale sono posati degli uccelli  disposti casualmente, in modo che alcuni guardano il loro vicino di destra e altri quello di sinistra. Ipotizziamo che il numero di uccelli sia sufficientemente grande, quanti uccelli sono osservati da uno, due o nessuno dei loro vicini? Nell’esempio qui sotto sono stati disegnati 72 uccelli, disposti casualmente, che guardano a destra o a sinistra.

1. SOLUZIONE. Con un numero sufficientemente grande di uccelli collocati a caso sul filo, il 50% di loro sarà guardato da un solo vicino, il 25% da due vicini e il restante 25% da nessun vicino. E’ come lanciare una moneta due volte, provando un numero sufficientemente grande avremo: il 50% una testa e una croce; il 25% due teste e il 25% due croci. 

2. Tom ha usato 14 mattoni per costruire un recinto per la sua nuova tartaruga, come disegnato in figura. Ora che la tartaruga è cresciuta, Tom vuole allargare il recinto il più possibile usando lo steso numero di mattoni. Come può fare?

2. SOLUZIONE. Il recinto più grande è quello più simile a un cerchio,  come proposto in figura.

3. Una corda lunga 20 metri lega Fido a un grosso albero del diametro di 2 metri. Il cane può quindi scorrazzare all’interno di un cerchio con un raggio di 21 metri, in parte occupato da una baracca che riduce l’area in cui può muoversi. Riuscite a calcolare di quanto è ridotta l’area di movimento di Fido rispetto al cerchio grande? Inoltre, secondo voi, Fido riuscirà a raggiungere l’invitante osso che si trova nella posizione mostrata in figura?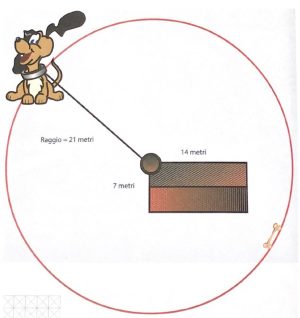

3. SOLUZIONE. A causa della presenza della baracca, Fido può muoversi solo nell’88% dell’area del cerchio grande. Purtroppo l’osso si trova proprio nel 12% fuori dalla sia portata, per cui Fido non potrà raggiungerlo.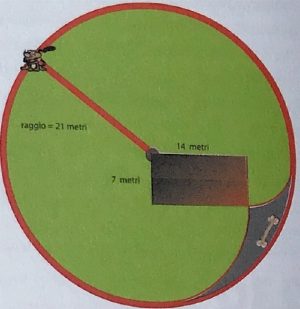

4. Ci sono 41 uomini disposti in cerchio. A partire da una determinata posizione sarà ucciso ogni terzo uomo. In quale posizione dovrebbe trovarsi Giuseppe nel cerchio per sopravvivere? E se volesse salvare anche la vita del suo migliore amico, dove dovrebbe collocarlo?

4. SOLUZIONE. Giuseppe e il suo amico, per salvarsi, dovrebbero trovarsi al 16º e 31º posto dal quale inizia il conteggio. Ad esempio se iniziamo a contare dalla posizione zero, il primo uomo a essere eliminato sarà il 3º poi il 6º, il 9º e via di seguito, allora si salveranno il 16º e 31º uomo. Se il conteggio iniziasse dalla posizione 1, quindi il primo eliminato sarebbe il 4º poi il 7º, il 10º ecc. allora resterebbero il 17º e il 32º. In sintesi occorre aggiungere 16 e 31 al numero dal quale si parte, infatti il testo del problema “A partire da una determinata posizione…” indica un riferimento relativo e non assoluto quindi Giuseppe, per avere la certezza di salvarsi, dovrebbe conoscere il numero di inizio del conteggio e di conseguenza scegliere dove collocarsi. 

L’amico Giorgio Vecchi, appassionato solutore e creatore di giochi matematici, ha proposto un’interessante variante: “Ci sono N uomini disposti in cerchio, con N > 3. Partendo dal numero 1 che è il primo a morire e saltando ogni volta 2 vivi, quindi il successivo a morire è il 4, poi il 7, il 10 ecc. e andando avanti fino a che rimangono due sopravvissuti, qual è il più piccolo valore di N affinché tra i due sopravvissuti ci sia proprio l’N-esimo?”

SOLUZIONE. Il più piccolo numero di uomini è 14. Gli eliminati sono: 1 – 4 – 7 – 10 – 13 – 3 – 8 – 12 – 5 – 11 – 6 – 2. Restano quindi 9 e 14, quindi con N = 14 si verifica che il 14° uomo sopravvive.

5. L’immagine sotto mostra un bicchiere pieno d’acqua fino all’orlo e una mano con una monetina da un centesimo. Quanti monetine posso introdurre nel bicchiere prima che l’acqua fuoriesca dal bordo?

5. SOLUZIONE. La risposta fornita mediamente dal pubblico è 4 o 5 monetine ma, incredibilmente, si può arrivare fino a 60 monetine. Nell’esperimento, svolto da Nobuyuki Yoshigahara (un’altra leggenda dei giochi logici)  durante una colazione amicale con Ivan Moscovich, l’acqua traboccò dopo 63 monetine inserite. Nobuyuki, con grande pazienza, inserì le monetine lentamente sul pelo dell’acqua e raggiunse questo straordinario risultato. Il fenomeno si verifica a causa della tensione superficiale dell’acqua. Le molecole dell’acqua esercitano una forte attrazione reciproca e la superficie si comporta come una membrana elastica. Con l’introduzione delle monete, questa membrana si tende notevolmente prima di rompersi, formando una superficie incurvata verso l’esterno.

Per chi volesse approfondire il tema della tensione superficiale dell’acqua, suggeriamo un ulteriore esperimento. Riuscite a far “galleggiare” sul pelo dell’acqua una vecchia moneta da 10 lire o da 5 lire, posizionandola con molta attenzione ad esempio utilizzando una carta assorbente o una semplice forchetta?

A lunedì prossimo.