
I Giochi del Lunedì di Prisma del 22 maggio 2023 a cura di Fabio Ciuffoli
La rassegna di oggi è dedicata a Ivan Moscovich, una leggenda nel mondo dei giochi logici e matematici, che ci ha lasciato un mese fa all’età di 96 anni. Ivan è stato un prolifico inventore di giochi e di giocattoli, un pioniere dei musei scientifici interattivi e un autore di libri bestseller. I seguenti problemi sono tratti dal suo libro The Big Book of Brain Games, che ha venduto circa mezzo milione di copie. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le soluzioni.
Dedicato a Ivan Moscovich
1. Immaginate un filo lunghissimo sul quale sono posati degli uccelli disposti casualmente, in modo che alcuni guardano il loro vicino di destra e altri quello di sinistra. Ipotizziamo che il numero di uccelli sia infinito, quanti uccelli sono osservati da uno, due o nessuno dei loro vicini? Nell’esempio qui sotto sono stati disegnati 72 uccelli, disposti casualmente, che guardano a destra o a sinistra.
2. Tom ha usato 14 mattoni per costruire un recinto per la sua nuova tartaruga, come disegnato in figura. Ora che la tartaruga è cresciuta, Tom vuole allargare il recinto il più possibile usando lo steso numero di mattoni. Come può fare?
3. Una corda lunga 20 metri lega Fido a un grosso albero del diametro di 2 metri. Il cane può quindi scorrazzare all’interno di un cerchio con un raggio di 21 metri, in parte occupato da una baracca che riduce l’area in cui può muoversi. Riuscite a calcolare di quanto è ridotta l’area di movimento di Fido rispetto al cerchio grande? Inoltre, secondo voi, Fido riuscirà a raggiungere l’invitante osso che si trova nella posizione mostrata in figura?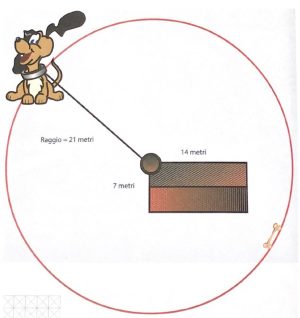
4. Ci sono 41 uomini disposti in cerchio. A partire da una determinata posizione sarà ucciso ogni terzo uomo. In quale posizione dovrebbe trovarsi Giuseppe nel cerchio per sopravvivere? E se volesse salvare anche la vita del suo migliore amico, dove dovrebbe collocarlo?
5. L’immagine sotto mostra un bicchiere pieno d’acqua fino all’orlo e una mano con una monetina da un centesimo. Quanti monetine posso introdurre nel bicchiere prima che l’acqua fuoriesca dal bordo?
Aggiornamento per le soluzioni click qui.
I problemi sono tratti dal suo libro Matematica il grande libro dei giochi di Ivan Moscovich. Il n. 4 “Le permutazioni di Giuseppe Flavio” è un problema di matematica collegato ad un episodio autobiografico raccontato dallo storico ebreo Flavio Giuseppe nella sua opera Guerra Giudaica composta tra il 93 e il 94 d.C.
Nell’immagine in evidenza Harmogram di Ivan Moscovich
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
11 risposte
1. Se la disposizione è casuale direi che il 25% è guardato da 2, il 25% da nessuno e il 50% da uno solo
Problema 3 vedi immagine allegata.
1. Immaginando tre uccelli posizionati nello stesso verso, ho, rispetto a quello centrale 4 posizioni:
a: i laterali guardano entrambi a destra (DD) e l’uccello centrale è osservato da tutti e due;
b: i laterali guardano entrambi a sinistra (SS) e l’uccello centrale non è osservato da nessuno dei due;
c: uno guarda a destra l’altro a sinistra (DS o SD) e l’uccello centrale è osservato solo da 1.
DD, SS DS e SD hanno probabilità 1/4, quindi 1/4 degli uccelli è osservato da 2, 1/4 da nessuno e metà da 1. In media 1/4*2+1/2*1=1, ogni uccello è osservato da un altro.
Perfetto. A domani per le soluzioni.
2. A parità di lati, il poligono che ha l’area maggiore è il cerchio: quindi disporrei i mattoni in modo da ottenere un poligono con 14 lati che approssima il cerchio.
3.Fido arriva all’angolo in basso a destra della baracca e non raggiunge l’osso (non ripeto formule già scritte, la mia è uguale). L’area iniziale è 441 pi e si riduce a 3/4*441 pi+14^2/4*pi+7^2/4 pi=392 pi, che vale 88,8% dell’area iniziale.
4. Facendo la simulazione, partendo da 1, rimangono due persone il numero 16 e il numero 31; Giuseppe può scegliere per se la posizione n.31 e per il suo amico la numero 16;
5. Usando delicatezza e sfruttando la forza di adesione e coesione delle molecole d’acqua riesco ad inserire anche decine di monetine (anche 60) da 1 centesimo; poi ad un certo punto le molecole si sganciano e l’acqua fuoriesce.
Problema 2 della tartaruga. Tom deve costruire un recinto di 14 lati.
n. 3. ((Pi*R^2)/4)-((Pi*7^2)/4)-((Pi*14^2)/4)-(7*14)+(7*14). Non riuscirà
Problema 3.
Se non ci fosse il vincolo della baracca il cane avrebbe a disposizione un’area di 440*PI, considerando tutto il cerchio di raggio 21 meno l’albero di raggio 1.
La baracca (e la catena!) limita gli spostamenti al suo retro, per cui ho calcolato che l’area a disposizione si riduce al 86,65% del totale calcolato prima.
In altri termini, il cane si vede ridotta l’area di movimento di 13,35% e NO, non riuscirà a raggiungere l’invitante osso.
Problema 1. La metà degli uccelli sarà osservata da uno, un quarto da due e un quarto da nessuno.
Problema 2.
Visto che sono già disposti in modo da massimizzare l’area di un rettangolo, ipotizzo che possiamo allontanarci da un recinto rettangolare. Quindi li metterei tutti in cerchio(in realtà poligono regolare di 14 lati): area massima a parità di perimetro.
Poi, se si può, li spezzerei e farei un poligono di 28 lati, ecc. fino al cerchio limite…
Ottimo. A domani per le soluzioni.