Menu
Soluzioni dell’8 maggio 2023 a cura di Fabio Ciuffoli
Ieri abbiamo presentato tre problemi di geometria proposti sul canale You Tube da “Fun with Maths”, un gruppo di brillanti animatori e divulgatori matematici. Di seguito pubblichiamo le nostre proposte di soluzione.
“Fun with Maths” tre problemi di geometria – soluzioni
1. Un quadrato è stato suddiviso in quattro quadrilateri. Calcolare l’area del quadrilatero verde.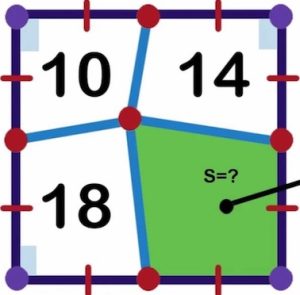
1. SOLUZIONE. Due quadrilateri opposti sono metà dell’area totale quindi S + 10 = 18 + 14 perciò S = 22. Estremizzando, se il punto centrale coincidesse con un angolo del quadrato, avremmo tre triangoli di cui il centrale è il doppio degli altri.
Un altro metodo di soluzione considera il quadrato composto da otto triangoli a coppie equivalenti avendo basi e altezze congruenti. Utilizzando i simboli in figura avremo: S1 + 2S2 + 2S3 + S4 = 42 da cui S1 + S4 = 42 – 2(S2 + S3) che diviene S1 + S4 = 42 – 2 · 10 = 22.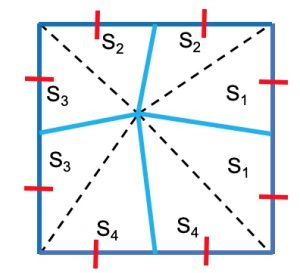 
2. Calcolare l’area ombreggia in verde interna a un rettangolo.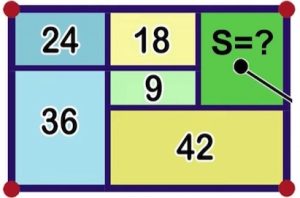
2. SOLUZIONE. Ci sono diversi metodi per la soluzione di questa tipologia di problemi. Abbiamo scelto quello proposto da Massimo Molinelli che utilizza le proporzioni, dividendo il rettangolo giallo, in basso a destra, in due parti B e 42 – B.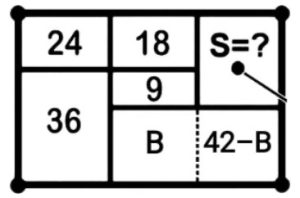 
Avremo 18 : 24 = (9 + B) : 36 da cui (9 + B) = 36 • 18 / 24 quindi B = 18.
Inoltre S : (9 + 18) = (42 – B) : B da cui S = 27 • 24 / 18 = 36.
3. Calcolare la lunghezza del lato AD del rettangolo.
3. SOLUZIONE. I due rettangoli sulla sinistra hanno il lato orizzontale (58 + 29) / 15 = 5,8. Ora possiamo calcolare i rispettivi lati verticali che sono 5 e 10.
Allo stesso modo, i due rettangoli a destra hanno il lato orizzontale (54 + 27) / 15 = 5,4 quindi i rispettivi lati verticali 10 e 5.
A questo punto possiamo dedurre che i tre rettangoli centrali hanno la stessa altezza, che è 5, per cui la loro larghezza è 44 / 5 = 8,8. Infine sommando otteniamo la lunghezza richiesta: 5,8 + 8,8 + 5,4 = 20.
Per chi fosse interessato, pubblichiamo la soluzione del problema nell’immagine in evidenza.
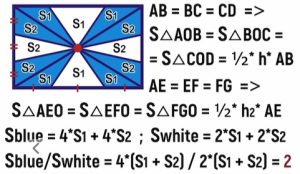
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).