I Giochi del Lunedì di Prisma del 8 maggio 2023 a cura di Fabio Ciuffoli
Oggi presentiamo tre problemi di geometria proposti sul canale You Tube di “Fun with Maths”, un gruppo di brillanti animatori e divulgatori matematici. Invitiamo i lettori a inviare osservazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le nostre proposte di soluzione.
“Fun with Maths” tre problemi di geometria
1. Un quadrato è stato suddiviso in quattro quadrilateri. Calcolare l’area del quadrilatero verde.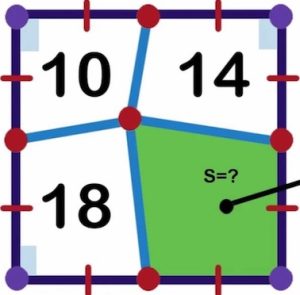
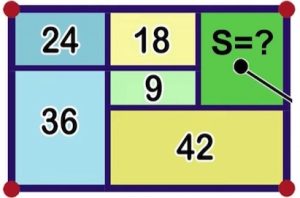
2. Calcolare l’area ombreggia in verde interna a un rettangolo.
3. Calcolare la lunghezza del lato AD del rettangolo.
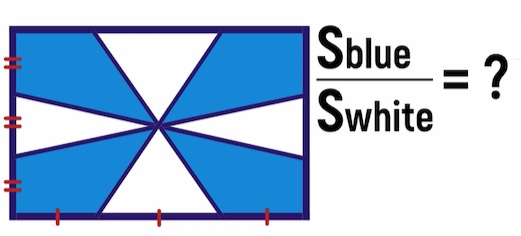
Per chi fosse interessato, nell’immagine in evidenza, abbiamo riportato un altro problema di geometria da “Fun with Maths” in cui si chiede il rapporto tra la superficie blu e la superficie bianca di una bandiera.
Aggiornamento per le soluzioni click qui.
I problemi sono stati proposti da Fun with Maths, che ringraziamo per il lavoro svolto e la disponibilità. Math Olympiad Questions. Learn how to solve Math Olympiad Problems easily
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
30 risposte
1: Anche le risposte 58 e 102 vanno bene visto che il disegno è completamente sproporzionato.
Direi che qualsiasi soluzione in cui
a*a=10,5 + X/4
a = semilato
X = area che manca
va bene.
Quindi infinite soluzioni.
Ti riferisci al problema 1?
Soluzione 3 formule
Soluzione 3
Soluzione problema 2 bis
Soluzione problema 2 in due allegati
Le risposte sono:
2
32
36
20
Lo svolgimento è allegato
Ottima grafica e procedimento, ma c’è una distrazione al problema 1. A domani per le soluzioni commentate.
si.
22 e non 32
mi correggo 22 e non 32
Mi correggo lato 20
Problema 1 area 22
Problema 2 mi sembra che l’area verde sia congruente a 18 e 9…quindi area 27
Problema 3 sommando tutte le aree ottengo 300…divido per 15 e ottengo area 20
Bene 1 e 3. Sulla 2 c’è qualcosa da rivedere. A domani per le soluzioni commentate.
3) b₁ = (58+29)/15 = 29/5;
b₃ = (27+54)/15 = 27/5;
58 : b₁ = (A₁+44) : b₂
27 : b₃ = A₁ : b₂ ⇒ A₁ = 27•b₂/(27/5) = 5b₂;
58 : (29/5) = (5b₂+44) : b₂
(29/5)(5b₂+44) = 58b₂;
b₂ + 44/5 = 2b₂;
b₂ = 44/5;
AD = b₁ + b₂ + b₃ = (1/5)(29+44+27) = 100/5 = 20u
3 ) Area totale = 15 × 11 = 165
Area verde = 165 – ( 60+69 )=
165 – 129 = 36
Problema 2
Quesito 3. (58+29) / 15 + 44 / (15/3) + (27+54) / 15 =
87/15 + 44/5 + 81/15 =
5,8+8,8+5,4=20
Problema 3) AD=A:h. Perciò 300/15=20
2. A mente, 100/5, ovvero 20
N. 2. (21-9)×3=36
1) 8^2 = 64
64- ( 10+14+18 )
64- 42 = 22 Area verde
Ottimo. A domani per le soluzioni commentate.
Anche io ho pensato questo, ma mi chiedo: dove si capisce che il lato è 8? Lo intuisco perché vogliamo fare venire l’area di 64?
Non so quale procedimento abbia seguito Marco. In ogni caso sappiamo che metà dell’area del quadrato è data dalla somma dei due quadrilateri opposti (14 + 18 = 32) per cui l’area del quadrato è 64, quindi il lato 8.
Rispondo al problema dell’immagine nell’intestazione.
Il rapporto S(blue)/S(white) è uguale a 2.
La dimostrazione è tracciare le diagonali del rettangolo e osservare che su ogni lato insistono tre triangoli uguali, di cui due blu e uno bianco.
Ottimo. A domani per le soluzioni commentate.
Bella, intuitiva e sintetica.
Problema 3. AD= 8,8+5,8+5,4 =20
1. 22
2. 36
3. 20
S(blue)/S(white) = 2
Perfetto. A domani per le soluzioni commentate.