85. Soluzione del 13 marzo 2023 – Il Gioco del MIU

La soluzione del 13 marzo 2023 a cura di Fabio Ciuffoli

Ieri abbiamo presentato il Gioco del MIU ideato Douglas R. Hofstadter, scienziato cognitivo esperto di intelligenza artificiale, insegnante al Massachusetts Institute of Technology negli USA. Di seguito pubblichiamo la soluzione proposta dall’autore con qualche riflessione.  

Il Gioco del MIU – soluzione 

Il gioco utilizza solo tre lettere dell’alfabeto: M, I, U. Con queste tre lettere è possibile produrre sequenze, denominate stringhe, come ad esempio MU oppure IUMMU o UMIMI, ecc. Il gioco consiste nel partire dalla stringa MI per arrivare a produrre la stringa MU, tenendo conto delle seguenti quattro regole:

Regola i.  Da una stringa che termina con una I si può aggiungere una U alla fine. Ad esempio da MI si può ottenere MIU, oppure da MIUI si può ottenere MIUIU e via di seguito.

Regola ii. Da una stringa del tipo Mx si può ottenere Mxx. Ad esempio da MI si può ottenere MII poi MIIII, oppure da MIU si può ottenere MIUIU e via di seguito.

Regola iii. In una stringa dove c’è III si può sostituire con U. Ad esempio da UMIIIMU si può ottenere UMUMU oppure da MIIII si può ottenere MIU o anche MUI, da MIII si può ottenere MU, da IIMII non si può ottenere nulla di nuovo perché le tre I devono essere in fila. Non si può usare questa regola all’indietro e quindi da MU ottenere MIII, perché tutte le regole funzionano a senso unico.

Regola iv. In una stringa dove c’è UU si può eliminarlo. Ad esempio da MUUUI si può ottenere MUI, da MUUU si può ottenere MU.

Le prime due regole allungano e le ultime due accorciano la sequenza, come riassunto nel riquadro seguente.

E’ possibile produrre la sequenza MU a partire da MI?

Ecco qualche suggerimento. In genere si inizia derivando un certe numero di stringhe completamente a caso come proposto di seguito. Abbastanza presto ci si accorge che tutte le stringhe cominciano con M, infatti le quattro regole hanno questa proprietà ….. Lasciamo al lettore le ulteriori considerazioni.

SOLUZIONE. Le risposte arrivate in redazione sono state ottime sia per le argomentazioni che per la chiarezza. Di seguito esponiamo una spiegazione del problema attenendoci alla proposta dell’autore Douglas Hofstadter che introduce gradualmente il metodo Meccanico, Intelligente e Ulteriore (appunto MIU) fino alle discipline Zen.

Dopo qualche tentativo, ci accorgiamo di alcune caratteristiche del sistema. Ad esempio, tutte le stringhe cominciano con M, infatti le regole hanno questa proprietà. C’è qualcosa di molto significativo in questa osservazione: essa rivela una delle differenze tra uomo e macchina. L’uomo ha la capacità di osservare ciò che sta facendo, così intuisce quali sono i problemi del suo operato, cosa che, a certi livelli, manca alla macchina. 

A questo punto possiamo definire due modi di lavoro: il Modo Meccanico (modo M) quello di lavorare all’interno del sistema e il Modo Intelligente (modo I) quello di operare dall’esterno il sistema. Per completezza accenneremo anche a una terza possibilità, chiamata Modo Ulteriore (modo U) che è l’atteggiamento tipico delle filosofie Zen.

Il Modo Meccanico

Il Modo Meccanico prevede di operare all’interno del sistema. Partendo dalla stringa iniziale MI si vagliano tutti i casi possibili. A partire da MI si possono applicare: la regola i per ottenere MIU; la regola ii per ottenere MII. Da MIU si può applicare la regola ii ed ottenere MIUIU; da MII applicando la regola i si può ottenere MIIU e con la regola ii  si può ottenere MIIII e via di seguito come proposto in figura.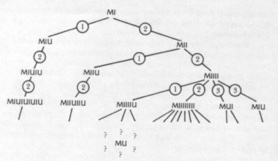

Questo metodo produce ogni possibile stringa poiché le regole vengono applicate in ogni ordine concepibile. Tuttavia non è chiaro quanto tempo si debba aspettare prima che una data stringa compaia nell’elenco e se, nel nostro caso, la stringa MU appartenga o no al sistema MIU. Il Modo Meccanico porta, anche se in tempi lunghi e con calcoli complicati, alla soluzione del problema, ma si rivelerà un metodo inadeguato. Proponiamo quindi di pensare ad un’altra procedura che chiameremo Modo Intelligente.

Il Modo Intelligente

Il Modo Intelligente prevede una riflessione sulle regole di derivazione. Partiamo da MI. Già sappiamo che M sarà sempre l’iniziale di tutte le stringhe producibili, a questo punto ci chiediamo se è possibile eliminare la I. Le regole i e iv sono ininfluenti sulle I. Le regola ii produce delle I raddoppiandole e la regola iii le elimina in ragione di tre alla volta. Sta di fatto che a partire da MI e raddoppiando si ottiene MI, MII, MIIII. MIIIIIIII e via di seguito, la serie delle I è 1, 2, 4, 8, 16, 32, …  che non è mai divisibile per tre, per cui non è possibile eliminare tutte le I. In breve la regola ii, raddoppiando le I a partire da un numero non multiplo di 3, non crea mai un multiplo di tre, quindi la risposta è che MU non appartiene al sistema MIU

Si noti come il rompicapo delle I-somme, di per sé non complicato, era reso difficile dall’azione incrociata delle regole per accorciare e per allungare. Prima di analizzare dall’esterno il problema potevamo immaginare che, combinando le regole con un abile andirivieni, saremmo riusciti a raggiungere lo zero. Ora, grazie a un semplice ragionamento aritmetico, sappiamo che ciò non è possibile.

Abbiamo visto che dall’interno del sistema, con il modo che abbiamo chiamato Meccanico, si può operare fino ad un certo livello, mentre  dall’esterno del sistema, con il modo Intelligente, siamo pervenuti rapidamente alla soluzione del problema. Ora, in progressione e alla ricerca di metalinguaggi, affrontiamo un Modo Ulteriore che può aprire nuove prospettive e allargare gli orizzonti concettuali e percettivi.

Il Modo Ulteriore

Un Modo Ulteriore di approccio ai sistemi formali viene proposto dalle discipline Zen. Lo Zen si propone, attraverso la meditazione e l’illuminazopne, la liberazione della mente e il raggiungimento di una eterna rinascita. Può accadere a chiunque, in un momento folgorante qualcosa si apre e siamo nuovi in ogni fibra, vediamo lo stesso non-più-stesso mondo con altri occhi. Questo potere di rinnovare l’universo è dato dalla grazia, non dalla logica. Credere che le parole conducano alla verità equivale a credere che un sistema formale incompleto conduca alla verità. Un sistema formale condurrà a qualche verità, tuttavia, per quanto potente sia non può condurre a tutte le verità.

Uno strumento per avvicinarsi all’illuminazione è il koan. I koan sono composizioni brevi, abbastanza oscure, scritte sotto forma di racconti o poesia e commenti. Hanno la funzione di sospendere la ragione calcolante e di rompere le sequenze logiche. Ecco un koan  per riflettere sul gioco MU.

Koan n. 1. “Il cane di Joshu”.   

Un monaco domandò a Joshu, un maestro cinese di Zen: “Un cane ha natura Buddha o no?”.

Joshu rispose: “Mu” (Mu in cinese vuol dire ‘Niente’ o ‘No’).

 Commento di Mumon.

Per realizzare lo Zen bisogna oltrepassare la barriera dei patriarchi. L’Illuminazione viene sempre dopo che la strada del pensiero è bloccata. Se non superate la barriera dei patriarchi o se la vostra strada del pensiero non è bloccata, qualunque cosa pensiate, qualunque cosa facciate è come uno spettro che vi intralci. Domanderete: Che cos’è la barriera di un patriarca? E’ questa sola parola, Mu.

Questa è la barriera dello Zen. Se voi la superate vedrete Joshu faccia a faccia. Allora potrete lavorare mano nella mano con l’intero lignaggio dei patriarchi. Non vi sembra una bella cosa?

Se volete superare questa barriera, dovete lavorare con tutte le ossa del vostro corpo, con tutti i pori della vostra pelle, colmi di questa domanda: Che cosa è Mu? e tenerla dentro di voi giorno e notte. Non crediate che sia il consueto simbolo negativo che significa niente. Non è il nulla, il contrario dell’esistenza. Se volete veramente superare questa barriera, dovete sentirvi come se beveste una palla di ferro rovente che non potete ne inghiottire ne sputare. Allora la minore conoscenza che avevate prima scompare. Come un frutto che matura al tempo giusto, la vostra soggettività e la vostra oggettività diventano naturalmente una cosa sola. E’ come un muto che abbia fatto un sogno. Lui sa che cosa ha sognato, ma non può raccontarlo. Quando egli entra in questa condizione, il guscio del suo io si spacca, e lui può scuotere il cielo e muovere la terra. E’ come un grande guerriero dalla spada affilata. Se un Buddha sta sulla sua strada, lui lo abbatte; se un patriarca gli oppone un ostacolo, lui lo uccide e a suo modo sarà affrancato dalla nascita e dalla morte.

Potrà entrare in qualunque mondo come se fosse il suo campo di gioco. Come potrete riuscirci anche voi ve lo dirò con questo Koan:

Concentrate tutta la vostra energia in questo Mu e non concedetevi la minima interruzione. Quando sarete entrati in questo Mu e non ci saranno interruzioni, ciò che avrete ottenuto sarà come una candela che arde ed illumina l’intero universo.

         Un cane ha la natura Buddha?

         Questa è la più seria di tutte le domande.

         Se tu dici di sì, se tu dici di no,

         Perdi la tua propria natura-Buddha.

A lunedì prossimo.