
Le soluzioni del 14 novembre 2022 a cura di Fabio Ciuffoli
Ieri abbiamo presentato quattro problemi di geometria proposti da Catriona Shearer, insegnante e appassionata divulgatrice di matematica e di seguito pubblichiamo le soluzioni .
La geometria a colori di Catriona – soluzioni
1. I quattro triangoli colorati sono equilateri. Quale rapporto c’è tra l’area dei triangoli colorati e l’area del rettangolo? 1. SOLUZIONE. Un triangolo equilatero ha tre angoli di 60 gradi, perciò i quattro triangoli bianchi hanno l’angolo, al centro della croce, di 30 gradi, così da comporre l’angolo giro di 360 gradi, come mostrato nella figura seguente. Consideriamo il triangolo bianco in alto a sinistra, che ha l’angolo in alto a sinistra di 30 gradi, perché dall’angolo retto vanno sottratti 60 gradi. Questo triangolo è isoscele, perciò il lato a è uguale al lato del triangolo equilatero rosso e quindi il lato superiore del rettangolo è 3a. Allo stesso modo, considerando il triangolo bianco in basso a sinistra, determiniamo l’altezza del rettangolo che è 2b.
1. SOLUZIONE. Un triangolo equilatero ha tre angoli di 60 gradi, perciò i quattro triangoli bianchi hanno l’angolo, al centro della croce, di 30 gradi, così da comporre l’angolo giro di 360 gradi, come mostrato nella figura seguente. Consideriamo il triangolo bianco in alto a sinistra, che ha l’angolo in alto a sinistra di 30 gradi, perché dall’angolo retto vanno sottratti 60 gradi. Questo triangolo è isoscele, perciò il lato a è uguale al lato del triangolo equilatero rosso e quindi il lato superiore del rettangolo è 3a. Allo stesso modo, considerando il triangolo bianco in basso a sinistra, determiniamo l’altezza del rettangolo che è 2b.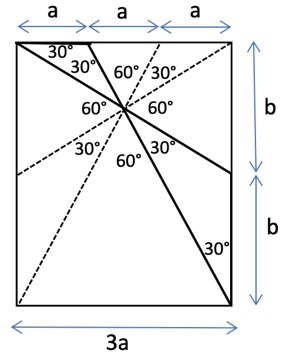 Ipotizziamo che l’area del triangolo equilatero rosso, di lato a, sia 1, allora anche i due triangoli isosceli adiacenti saranno di area 1, poiché hanno la stessa base e la stessa altezza, come mostrato nella figura seguente. Ora consideriamo il triangolo in alto in grassetto, composto dai tre triangoli, che ha area 3. Il triangolo equilatero giallo, a destra in grassetto, ha anch’esso area 3, poiché ha la base uguale e l’altezza uguale al triangolo composto da tre triangoli.
Ipotizziamo che l’area del triangolo equilatero rosso, di lato a, sia 1, allora anche i due triangoli isosceli adiacenti saranno di area 1, poiché hanno la stessa base e la stessa altezza, come mostrato nella figura seguente. Ora consideriamo il triangolo in alto in grassetto, composto dai tre triangoli, che ha area 3. Il triangolo equilatero giallo, a destra in grassetto, ha anch’esso area 3, poiché ha la base uguale e l’altezza uguale al triangolo composto da tre triangoli.
L’area del triangolo equilatero giallo a destra è la stessa del triangolo isoscele bianco in basso a destra, entrambi in grassetto nella figura seguente. Anche in questo caso hanno la base, b, uguale e l’altezza uguale. Il triangolo equilatero verde in basso ha il lato triplo rispetto al triangolo equilatero rosso in alto e poiché se il lato di un triangolo equilatero triplica, l’area aumenta di 9 volte, quindi ha area 9.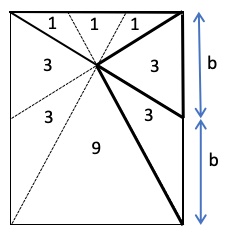 Ora sommiamo le aree dei triangoli equilateri: 1 + 3 + 9 + 3 = 16. L’area del rettangolo è 1 + 1 + 1 + 3 + 3 + 9 + 3 + 3 = 24. Infine 16/24 semplificato 2/3, l’area dei triangoli colorati è 2/3 dell’area del rettangolo.
Ora sommiamo le aree dei triangoli equilateri: 1 + 3 + 9 + 3 = 16. L’area del rettangolo è 1 + 1 + 1 + 3 + 3 + 9 + 3 + 3 = 24. Infine 16/24 semplificato 2/3, l’area dei triangoli colorati è 2/3 dell’area del rettangolo.
2. I tre rettangoli sovrapposti sono congruenti, ciascuno di area 4. I punti neri segnano i punti medi dei lati corti. Qual è l’area totale del disegno?
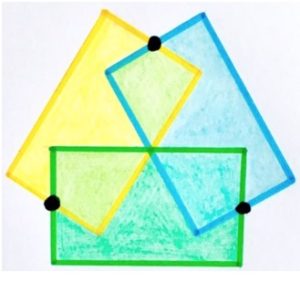 2. Soluzione. L’area in cui due rettangoli si sovrappongono può essere sezionata in due triangoli rettangoli uguali, ciascuno di area 1/8 del rettangolo, come mostrato in figura. L’area di ogni sovrapposizione è quindi 2 * (1/8) * 4 = 1. Infine l’area totale del disegno è 12 – 3 = 9.
2. Soluzione. L’area in cui due rettangoli si sovrappongono può essere sezionata in due triangoli rettangoli uguali, ciascuno di area 1/8 del rettangolo, come mostrato in figura. L’area di ogni sovrapposizione è quindi 2 * (1/8) * 4 = 1. Infine l’area totale del disegno è 12 – 3 = 9.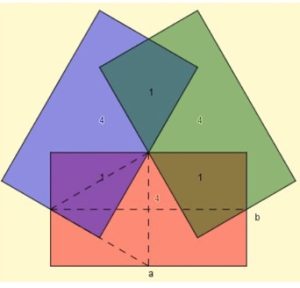
3. Due cerchi e due quadrati. Determinare l’area del quadrato piccolo.
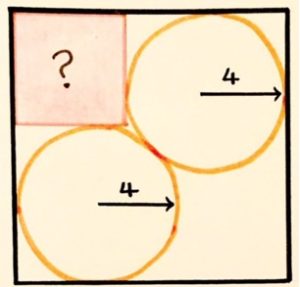
3. SOLUZIONE. Con il teorema di Pitagora calcoliamo la distanza tra il centro di una circonferenza e il vertice del quadrato grande, come mostrato in figura, AB = √ 42 + 42 = √ 32.
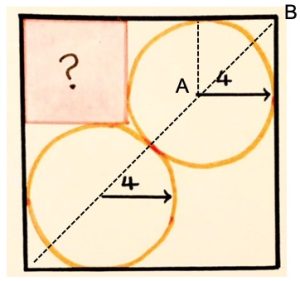
La diagonale del quadrato grande è 8 + 2√ 32, che diviene 8 + 8√2. Ora possiamo calcolare il lato del quadrato grande, dividendo la diagonale per √2, quindi (8 + 8√2) / √2 = 8/√2 + 8. A questo punto calcoliamo il lato del quadrato piccolo: 8/√2 + 8 – 8 = 8/√2. Ora elevando al quadrato troviamo l’area del quadrato piccolo (8/√2)2 = 32.
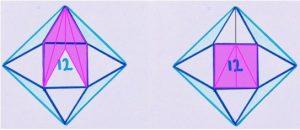
4. Quattro triangoli equilateri sono stati disegnati sui lati di un quadrato di area 12. Quanto misura l’area ombreggiata color celeste?
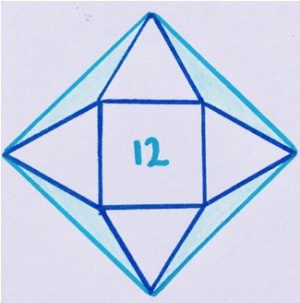
4. SOLUZIONE. Ricordiamo alcune formule per calcolare: Altezza del triangolo equilatero h = (√3/2) l; Area del quadrato nota la diagonale: d2/2.
Di seguito i disegni proposti da Catriona per la soluzione.
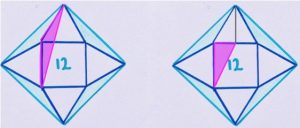
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).