
I Giochi del Lunedì di Prisma del 31 ottobre 2022 a cura di Fabio Ciuffoli
Oggi, prendendo spunto da due simboli antichissimi, presentiamo due giochi sul rapporto tra bellezza, armonia e matematica. “La bellezza matematica è una qualità che non può essere definita, non più di quanto la bellezza possa essere definita per l’arte, ma chi studia matematica, di solito, non ha difficoltà ad apprezzarla”. Così ebbe a dire Paul Dirac nel 1939. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione nello spazio riservato ai commenti. Alle ore 17.00 di domani pubblicheremo le soluzioni.
É la matematica armonia e bellezza!
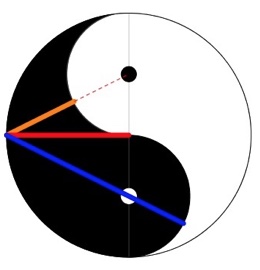
1. Yin Yang. Rappresentiamo il simbolo Yin-Yang in una circonferenza di diametro 2. La distanza tra i due centri dei cerchietti piccoli è uguale a 1. Calcolare la lunghezza del segmento arancione e del segmento blu.
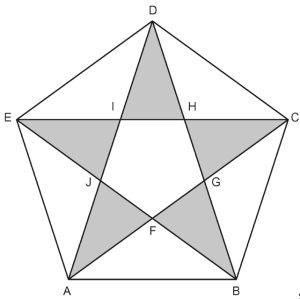
2. Pentagono regolare. In figura è disegnato un pentagono regolare di lato 1. Siete in grado di determinare il rapporto tra la diagonale AD e il lato AB?
Il disegno in copertina è di John Arioni, che ringraziamo per le sue ricerche e per il lavoro svolto.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
11 risposte
1 Osservo un triangolo equilatero,per cui il segmento arancione misura 0.5 e il segmento blu 1.5 .
2 Non sono sicura…mi sembra che il pentagono piccolo sia 1/4 del pentagono maggiore per cui il lato misura 0.25 ;Dopo alcuni calcoli il rapporto potrebbe essere 1.75/1 ?
Nel pomeriggio le soluzioni.
Yin yang: conoscendo il segmento rosso ed il raggio del cerchio piccolo con il teorema di Pitagora posso trovare la lunghezza del segmento che congiunge il vertice comune ai tre segmenti colorati e il cerchio piccolo. Aggiungendo a tale segmento il raggio del cerchio piccolo ottengo il blu invece sottraendolo ottengo l’arancione.
Ottimo. Nel pomeriggio le soluzioni.
Bene nel pomeriggio le soluzioni con dimostrazione.
1) Per simmetria ogni segmentino del diametro rappresentato in verticale è 0.5 cm, dunque il raggio dei cerchietti piccoli è 0.5 cm.
Con Pitagora segmento giallo = (Rad5)/2 – 1/2, o se si preferisce (rad5 – 1)/2.
Segmento blu (rad5 + 1)/2.
2) Ancora non so
Ottimo
Buongiorno a tutti. Il rapporto tra la diagonale e il lato = 1 di un pentagono regolare è uguale al rapporto aureo considerato un rapporto matematico armonioso tra valori particolari di lunghezze in cui viene suddiviso un segmento,…. noto già agli antichi matematici.
Di seguito la mia dimostrazione trigonometrica in due allegati.
Massimo Molinelli
1. Yin Yang. Si risolve ricordando il teorema della secante e della tangente. Il segmento rosso misura 1, inoltre la distanza tra i due centri è la somma dei raggi delle due circonferenze piccole, tra loro congruenti, dunque ciascuna di esse ha raggio che misura 1/2.
Per il segmento blu, applicando il detto teorema, avremo: blu : 1 = 1 : blu-1, proporzione che, come noto, definisce l’ inverso della sezione aurea del segmento unitario, cioè il cosiddetto rapporto aureo (1/φ)Blu:(rad(5)+1)/2.
Per evidente simmetria della situazione il segmento arancione misurerà allora quanto quello blu-1, cioè proprio φ, la sezione aurea: (rad(5)-1)/2.
La differenza tra arancione è blu è 2r. Detto questo, l’arancione x si calcola facilmente col teorema di Pitagora tra raggio rosso, e (x+r) che è l’ipotenusa.