
I Giochi del Lunedì di Prisma del 29 agosto 2022 a cura di Fabio Ciuffoli
Oggi proponiamo quattro giochi dedicati a Ennio Peres che il 17 luglio scorso, dopo breve malattia, ci ha lasciato. Già definito il “giocologo” più noto d’Italia, persona umile, generosa, dotata di un gradevole sensa di ironia, è stato un gigante della matematica divulgativa e dell’impegno civile. L’ultima volta l’ho incontrato a Firenze al convegno Pristem “Matematica e Gioco” nell’ottobre 2013. In quell’occasione gli chiesi di scrivere una breve presentazione al mio libro Giochi Matematici e Logici e gli lascai le bozze. Lui, gentile e disponibile, scrisse tre pagine bellissime che iniziano così:
Grazie ancora Ennio. Invitiamo i lettori a inviarci osservazione e proposte di soluzione utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le soluzioni.
Dedicato a Ennio Peres
1. Due triangoli e un cerchio. Conoscendo l’area del triangolo equilatero interno, evidenziato in figura, come è possibile determinare l’area del triangolo equilatero esterno?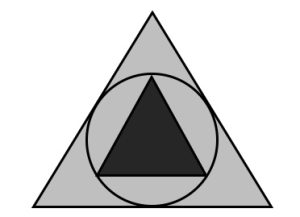
2. Matemagica. Pensate a due numeri da 1 a 10. Sommateli. Moltiplicate la somma per 10. Adesso aggiungete il più grande dei due numeri iniziali. Sottraete il più piccolo dei numeri iniziali. Ditemi il numero a cui siete arrivati e io vi dirò i numeri di partenza! Sapreste indicare il procedimento?
[Se volete rendere la sfida più difficile per voi e per il pubblico, magari utilizzando una calcolatrice, chiedete di scegliere i due numeri tra 1 e 100 e moltiplicate per 100 anziché per 10.]
3. Le insidie della statistica [vi chiediamo di fornire una risposta e una possibile motivazione]
A. Gli incidenti stradali avvengono prevalentemente in luoghi piuttosto vicini a quelli di residenza degli automobilisti che li provocano. Questo vuol dire che, per non rischiare di avere incidenti, è consigliabile allontanarsi molto dalla propria abitazione?
B. In base a uno studio condotto in una scuola elementare, è risultato che i bambini con i piedi più grandi sanno scrivere meglio di quelli con i piedi più piccoli. Questo significa che la dimensione dei piedi influenza l’abilità di scrittura?
C. In Arizona è stata rilevata una percentuale di persone affette da problemi respiratori molto più alta di quella riscontrata nel resto degli Stati Uniti. Questo significa che il clima dell’Arizona danneggia le vie respiratorie?
D. In seguito a un forte aumento demografico, in una città dell’Europa settentrionale si è rilevato anche un sensibile aumento di nidi di cicogne. Questo dato può rafforzare la credenza popolare secondo la quale le cicogne portano i neonati?
E. I cantanti di successo sono in prevalenza primogeniti. Questo significa che i primogeniti sono più intonati?
4. Quindici fiammiferi, perde chi preleva l’ultimo. Disponiamo sul tavolo 15 fiammiferi. Due giocatori, a turno, devono prelevare una quantità di fiammiferi compresa tra 1 e 4. Perde chi è costretto a prelevare l’ultimo fiammifero. Sapreste individuare una strategia vincente per il primo o per il secondo giocatore?
Aggiornamento per le soluzioni click qui.
I giochi sono tratti da “Un mondo di coincidenze” e “Matematica per comuni mortali” di Ennio Peres.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
21 risposte
Insidie della statistica.
A) è lapalissiano, una destinazione vicina comprende un percorso nelle vicinanze.
Una destinazione lontana comprende ANCHE un percorso nelle vicinanze.
Qualunque sia la destinazione, frequentiamo più spesso i luoghi vicini alla nostra abitazione.
B) una scuola accoglie studenti di età diversa. Assumendo una distribuzione uniforme degli altri fattori, al crescere dell’età si avrà una pratica più estesa nella scrittura, ma anche i piedi saranno mediamente più grandi.
C) correlazione debole.
Potrebbe essere addirittura vero il contrario, che le persone con problemi respiratori si trasferiscano in Arizona per beneficiare di un clima migliore.
D) può rafforzare la percezione comune che ci sia una correlazione, anche se una correlazione ovviamente non c’è. Le cicogne non portano i bambini.
E) lapalissiano anche qui. Essendo che esistono anche figli unici, il numero di primogeniti è ovviamente sempre superiore a quello dei secondogeniti e ancor più a quello dei terzogeniti.
Domanda 3. Le insidie della statistica
Tutte false. Ma interessante analizzare perché si collega con il discorso molto attuale di disinformazione diffusa.
A. Ovviamente tutte le auto saranno statisticamente più vicino alla residenza, I viaggi più lunghi sono più rari di quelli più corti (anche questo da verificare e quantificare). Dunque, la distanza è un fattore da usare come correzione statistica anziché elemento di correlazione.
B. I piedi diventano più grandi quando crescano e imparano a scrivere meglio.
C. Opposto: Le persone con problemi respiratori si trasferiscono in Arizona perché il clima è meglio. Dunque, per ogni studio di incidenza di malattie bisogna correggere per la parte delle persone malate che si trovano lì per la cura: È la stessa cosa di dire che in un ospedale ci sono più malati, dunque, è l’ospedale che fa ammalare le persone.
D. Le cicogne fanno I nidi su dei supporti particolari, spesso costruiti/creati dall’uomo (pali della luce, tralicci, tronchi d’alberi tagliati). Forte aumento demografico (che non significa in sé nascita di bambini ma semplicemente aumento di popolazione) potrebbe significare che sono stati costruiti nuovi quartieri con questi elementi presenti. Poi bisogna considerare il cibo che mangiano e dove vivano; in Europa del Nord si creano appositamente elementi Naturali in armonia con quartieri nuovi che potrebbero essere ospitali alle cicogne.
E. Bisogna vedere di quale paese si tratta, e come è la distribuzione dei primogeniti in generale rispetto a chi ha dei siblings: In alcune culture I primogeniti sono ormai la maggioranza; dunque, in qualsiasi professione la distribuzione sarà così. Se poi risulta comunque una professione con questa anomalia, beh, primogeniti potrebbero avere in famiglia dei fattori che influenzano sulla voglia di esibirsi ed esprimersi, dunque più che altro dei fattori culturali; la spiegazione potrebbe dunque essere tutto diverso.
Ottime considerazioni. Sono d’accordo sul tuo “discorso molto attuale sulla disinformazione diffusa” e direi in particolare sulle fallacie logiche del tipo “correlazione non implica causazione” oggi ampiamente utilizzate dai media e dai comunicatori di professione. Nel limiti del nostro spazio torneremo su questo argomento.
Ovviamente al link delle soluzioni ci sono tutte le spiegazioni. https://www.prismamagazine.it/giochi/58-soluzioni-del-29-agosto-2022-dedicato-a-ennio-peres/
Sulle insidie delle statistiche.
A) Significa che sono molto più frequenti i viaggi vicino casa (ad esempio il tragitto casa-lavoro)
B) Il piede di un bambino cresce con l’età come l’abilità nella scrittura.
C) Potrebbe essere che l’Arizona ha una minore densità di popolazione e l’incidenza delle malattie respiratorie risulta più elevata oppure l’incidenza della malattia nel resto degli USA è una media e quindi è semplicemente più alta della media ma non in valore assoluto.
D) Più nascite potrebbero portare a riscaldare maggiormente le abitazioni e favorire la nidificazione sui tetti più caldi.
E) Potrebbe essere semplicemente che nei primogeniti sono inclusi anche i figli unici.
Problema n. 2. Alla somma dei 2 numeri pensati, viene aggiunto uno zero, perché moltiplicato x 10.
Il posto dello zero, lo prende la differenza dei 2 numeri pensati, perché prima sommiamo il numero maggiore, poi sottraiamo il minore. La prima parte del numero, è la somma dei n. pensati. Quindi è da suddividere in modo che tra i due, ci sia la differenza, indicata dall’ultima cifra. E già che ci siamo, per n. da 1 a 100, si moltiplica x 100, qui la differenza la indica le ultime 2 cifre.
Da 1 a 1000 , x 1000, indicheranno le ultime 3 ecc. Ecc.
Saluti.
Rispondo al quesito 3 “Le insidie della statistica”.
A. Negli Stati Uniti la maggior parte degli incidenti avviene nel primo miglio da casa, in Europa nel primo chilometro… Suggerimento: parcheggiare a 2 chilometri da casa (2 miglia negli States) e rincasare a piedi. (Per la risposta vera mi associo ad Andrea).
B. In una scuola elementare bambini con i piedi MOLTO più grandi potrebbero essere pluriripetenti con poca voglia di studiare e quindi scrivere peggio degli altri.
C. La causa dei problemi respiratori in Arizona potrebbe essere il clima, ma potrebbe anche essere l’inquinamento, potrebbero essere i test nucleari nel deserto…
D. Forse la presenza di più bambini ha portato a scaldare di più le abitazioni e questo ha creato un habitat più favorevole alla nidificazione delle cicogne.
E. In Cina, dove si può avere al massimo un figlio, TUTTI i cantanti sono primogeniti!
In ogni caso potrebbe anche non esserci nessuna correlazione tra fenomeni apparentemente interdipendenti tra loro. Vedere per credere: http://tylervigen.com/spurious-correlations
Molto interessante il sito sulle correlazioni spurie. Il concetto di fallacia logica, nei diversi settori salute, politica, economia, società ecc. meriterebbe un approfondimento. In questa sede abbiamo semplicemente lo scopo di far nascere qualche dubbio e qualche domanda in più. Oggi pomeriggio le soluzioni abbastanza sorprendenti. Grazie per la segnalazione.
Problema 1. Il rapporto fra le aree non dipendono dai lati.
Pongo il lato del triangolo equilatero interno = 1, l’area del triangolo equilatero interno è (1^2/4)*radq(3); =radq3/4 quindi il raggio del cerchio r = 1/radq(3) e l’altezza del triangolo equilatero esterno è = radq3. Quindi il lato del triangolo equilatero esterno è uguale a 2×1 = 2 per cui l’area del triangolo equilatero esterno è radq(3) cioè 4 volte l’area del triangolo equilatero interno ( radq(3)/4)
Problema 1: il raggio del triangolo inscritto nella circonferenza è uguale all’apotema del triangolo circoscritto. Ora, visto che in un triangolo equilatero l’apotema e il raggio del triangolo sono in rapporto di 1 : 2, si ricava che il rapporto di similitudine k tra triangolo circoscritto e triangolo inscritto è uguale a 2. Pertanto, l’area del triangolo circoscritto è 2^2 = 4 volte quella del triangolo inscritto.
Problema 2: con un po’ di algebra sono arrivato a stabilire che il numero finale è 9x + 11 y. x è il numero più piccolo e y è il più grande.
A questo punto direi che dal numero finale tolgo 9 più volte fino ad arrivare a un numero multiplo di 11 (che riconosco facilmente perché o a doppia cifra uguale o se a tre cifre con le decine aumentate di 1 rispetto alle unità – es. 165 … 176 … 187 …). A quel punto ho sia il numero x (le volte che ho tolto 9) sia il numero y facendo la divisione per 11 del multiplo che mi resta dalle sottrazioni.
Quesito 3:
a – il buon senso mi direbbe che più strada faccio e più il rischio aumenta… ogni tratto del viaggio ha la stessa probabilità di avere incidenti (anche se esistono tratti più o meno pericolosi!), è solo che le strade vicino a casa le ripeto più volte.
b – Falso! Il piede si allunga con l’età, e con l’età e l’esercizio migliora la scrittura!
c – Falso perché potrebbe risentire di fattori ereditari…
Il d) e l’ e) non ho avuto il tempo di leggerli bene…
Quesito 4 – Per vincere di sicuro se sono il primo a muovere prendo 4 fiammiferi, mentre se sono il secondo – e il primo giocatore ha tolto meno di 4 fiammiferi – allora al mio turno ne tolgo quanti servono per lasciare 11 fiammiferi. In questo modo al prossimo pescaggio ne lascerò 6 e poi al terzo pescaggio 1 solo.
Tutti molto bene. A domani per le soluzioni.
1 Il triangolo esterno contiene 4 volte quello interno.
2 Nel risultato finale la cifra delle decine è la somma dei numeri scelti…la cifra delle unità la loro differenza.
4 Non esiste una strategia vincente.
Bella la tua soluzione al problema n.2! Tra l’altro anche algebricamente:
(10 + 1)x + (10 – 1)y = 10(x + y) + 1(x – y)
che prova esattamente la tua conclusione!
Ciao Andrea, a quale soluzione ti riferisci?
Alla soluzione del problema 2 di Cinzia De Ponti
Ok grazie
Bene 1 e 2. Il problema 4 prevede una strategia vincente per il primo giocatore. A domani per le soluzioni.
Bene 1 e 2. Il problema 4 prevede una strategia vincente per il primo giocatore. Domani pubblichiamo le soluzioni.
Dimostrazione grafica del problema 1.
Ruotando di 60°, a destra o a sinistra, il ∆ equilatero interno, si ottiene la figura indicata, in cui 4 triangolini equilateri congruenti formano il ∆ equilatero esterno.
Dunque l’area del triangolo ∆ equilatero esterno è 4 volte l’area di quello interno.
N. 1. Basta ruotare il triangolo interno di 60 gradi e si vede che si ottengono 4 equilateri uguali.
Al problema 1. Se il lato del triangolo equilatero interno è l, l’area del triangolo equilatero interno è (l^2/4)*sqrt3; quindi il raggio del cerchio r=l/sqrt3 e l’altezza del triangolo equilatero esterno è h=l*sqrt3. Quindi il lato del triangolo equilatero esterno è uguale a 2l per cui l’area del triangolo equilatero esterno è 4 volte l’area del triangolo equilatero interno