
Le soluzioni dell’11 aprile 2022 a cura di Fabio Ciuffoli
Ieri mattina abbiamo presentato sei giochi ideati dalla famiglia ucraina Grabarchuk e di seguito pubblichiamo le soluzioni.
Una straordinaria famiglia ucraina . soluzioni
1. Quale itinerario sulla cartina dell’Ucraina è più corto? Il verde: Uzhhorod – Lviv – Kyiv – Kharkiv. Il rosso: Khmelenytskyi – Odessa – Dnipro – Donetsk.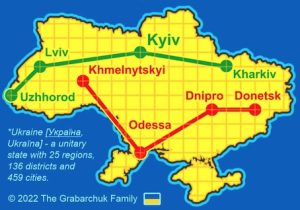
1. SOLUZIONE. Si calcolano i vari tratti con il teorema di Pitagora. L’itinerario rosso è leggermente più corto.
2. Quale forma può essere esattamente coperta dai quattro trapezi sulla destra?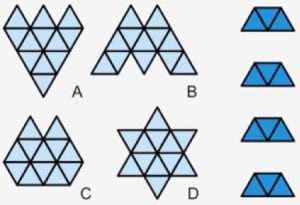
2. SOLUZIONE. La forma C. 
3. Quale triangolo ha l’area più grande?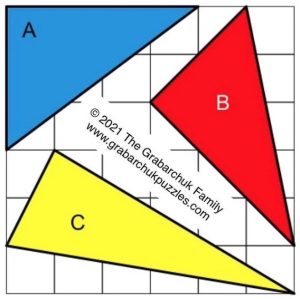
3. SOLUZIONE. La soluzione si può ottenere con diversi metodi. Possiamo calcolare l’area triangolo A 4*3/2 = 6u². Per gli altri due triangoli, possiamo procedere con Pitagora, calcolando i tre lati di ciascun triangolo e poi con il teorema di Erone trovare le rispettive aree. L’area di B ≈ 6u² e l’area di C ≈ 6,5 u². Il triangolo con l’area maggiore è C.
Un altro procedimento porta a calcolare l’area del rettangolo, in cui ciascun triangolo e inscritto e poi sottrarre le aree dei triangoli bianchi. Ad esempio, per il triangolo C si calcola l’area del rettangolo 6 * 3 e poi si sottrae l’area dei tre triangoli rettangoli di cateti 2-1, 6-1, 5-3.
Un ulteriore procedimento è l’utilizzo del teorema di Pick con il quale si può calcolare l’area di un poligono i cui vertici hanno, come nel nostro caso, coordinate intere.
4. In quale esagono l’area nera e l’area bianca sono uguali?
4. SOLUZIONE. Dividiamo l’area di ogni esagono regolare in tanti triangolini equilateri. La forma B è composta da 12 triangolini bianchi e 12 neri.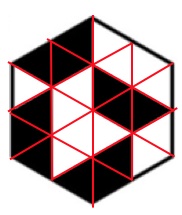
5. Quale figura ha l’area maggiore?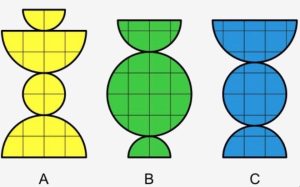
5. SOLUZIONE.
La figura B ha l’area maggiore.
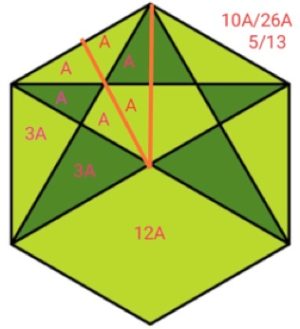
6. Quale il rapporto tra area verde scuro e verde chiaro?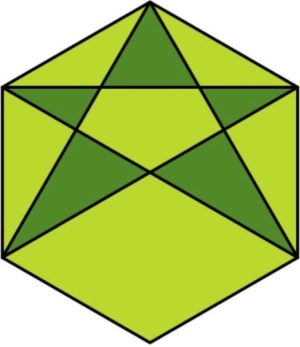
6. SOLUZIONE. Dividiamo idealmente l’esagono in sei triangoli equilateri e determiniamo le aree dei due colori per ciascun triangolo e infine calcoliamo il rapporto che è 5/13.
A lunedì prossimo
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
Una risposta
Segnalo la proposta di soluzione al problema n. 3 “Quale triangolo ha l’area più grande?” di Massimo Molinelli con illustrazione del Teorema di Pick: “Semplice col Teorema di Pick, dove si sfrutta la formula seguente: A = i + (p/2) – 1 dove A = area dei ∆; i = punti interni ai ∆; p = punti perimetrali dei ∆.
Dunque il △blu ha area 3 + (8/2) – 1 = 6; il △rosso ha area 4 + (6/2) – 1 = 6; il △giallo ha area 6 + (3/2) – 1 = 6,5.
I risultati possono essere interi o seminteri. I punti da considerare sono le intersezioni tra tutte le linee orizzontali con le verticali, all’interno o sul perimetro delle figure interessate; ogni quadratino è unitario.
Ugo Perillo ha aggiunto: “la cosa che mi ha sempre affascinato di questo teorema è che vale per qualsiasi poligono i cui vertici hanno coordinate intere”.
Grazie per la collaborazione.