Menu
Le soluzioni del 4 aprile 2022 – a cura di Fabio Ciuffoli
Ieri abbiamo proposto sei giochi di geometria a difficoltà crescente e ora presentiamo le soluzioni con dimostrazione.
Geometria da Maths, Reasoning, Knowledge – soluzioni
1. Determinare l’area colorata in blu sapendo che AB unisce i punti medi dei due lati del rettangolo.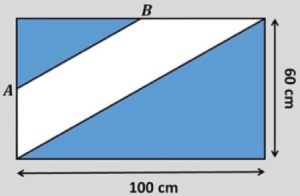
1. SOLUZIONE. Si calcolano le aree dei due triangoli rettangoli e poi si sommano: (100 * 60) /2 + (50 * 30) /2 = 3.750 cm2.
2. Determinare l’area colorata in blu.
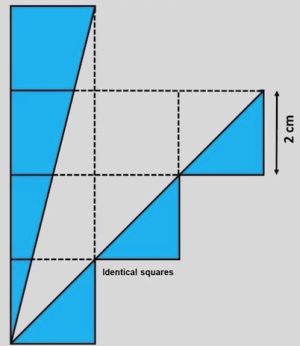2. SOLUZIONE. Si calcolano le aree dei quattro triangoli rettangoli e poi si sommano: (2 * 8) /2 + 3 (2 * 2 / 2) = 14 cm2.
3. Nella figura sono disegnati quattro cerchi con raggio rispettivamente di 6 cm, 4 cm, 3 cm e 2 cm. Determinare l’area colorata in blu.
3. SOLUZIONE. L’area blu più grande è data dalla differenza tra l’area dei cerchi rispettivamente di raggio 6 e di raggio 4. L’area blu più piccola è data dalla differenza tra l’area dei cerchi rispettivamente di raggio 3 e di raggio 2. Ora indicando con r1 = 6 cm, r2 = 4 cm, r3 = 2 cm e r3 = 1 cm, avremo:
Area blu = π (r12 – r22) + π (r32 – r42). Sostituendo: π (36 – 16) + π (9 – 4) = 25π.
4. Determinare l’area ombreggiata in blu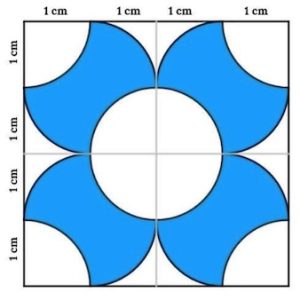
4. SOLUZIONE. Presentiamo due metodi per la soluzione. Consideriamo uno dei quattro quadranti di lato 2 cm, quello in alto a sinistra e indichiamo con A1A il quarto di cerchio colorato in verde e con A1B l’area colorata in rosso. Avremo: Area in blu di un quadrante = 2 A1A + 2 A1B.
Sostituendo: 2(πr2/4) + 2(r2 – πr2/4) = π/2 + (4 – π)/2 = 2 cm2. Moltiplicando l’area per 4 otterremo l’area totale in blu 4 * 2 = 8 cm2.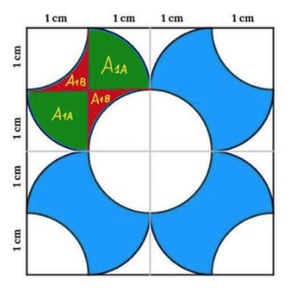
Un altro metodo, per la soluzione di questo problema, prevede la scomposizione e la ricomposizione della figura, come mostrato di seguito.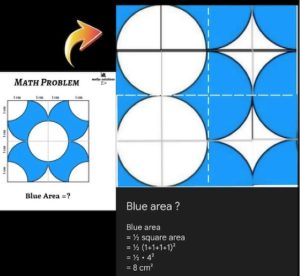
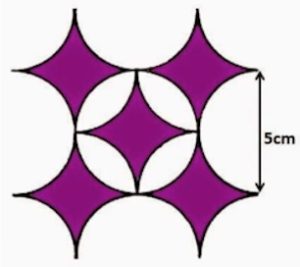
5. SOLUZIONE. Presentiamo la soluzione con scomposizione e ricomposizione della figura, con in calce i relativi calcoli.
6. Dal cubo con spigoli di 10 cm è stato tagliato il pezzo blu. Calcolare il volume della parte rimossa, sapendo che il taglio passa per i punti medi dei tre spigoli adiacenti.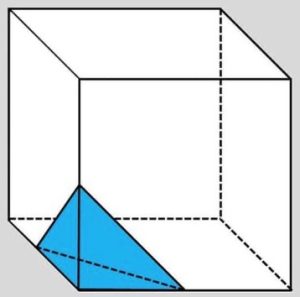
6. SOLUZIONE. La parte rimossa è un tetraedro irregolare, con quattro facce, quattro vertici e sei spigoli. Il volume di un tetraedro generato da tre vettori è uguale a 1/6 del volume del parallelepipedo generato dagli stesi vettori. Nel nostro caso è (5 * 5 * 5) / 6 = 20,83 cm3.
Per la prima soluzione del problema n. 4 abbiamo utilizzato un disegno di Massimo Molinelli, che ringraziamo per la disponibilità. A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
2 risposte
Massimo Molinelli ha scritto: “Una curiosità…. quando vengono troncati gli 8 vertici di un cubo con un piano perpendicolare alla diagonale che parte dal vertice da tagliare verso il vertice opposto allo stesso, secando nei punti di mezzo i tre spigoli che formano il vertice interessato,…. esso viene detto cubottaedro !!”
Segnalo di seguito l’intervento di Claudio Luciani sul gioco n 5, quello con l’area ombreggiata in viola, sintetico e chiarissimo:
“Ma quelle aree sono 5 quadrati da cui sottrarre un cerchio! 5L^2(1-π/4)”.