Menu
Le soluzioni del 21 marzo 2022 a cura di Fabio Ciuffoli
Ieri abbiamo presentato cinque problemi sugli enigmi di Mosca e ora pubblichiamo le soluzioni con le dimostrazioni.
Gli enigmi di Mosca – soluzioni
1. L’indovinello dell’oca. Un’oca solitaria stava volando in direzione opposta a uno stormo di oche. Passando gridò: “Salve, 100 oche!”. L’oca che era a capo dello stormo le rispose: “Noi non siamo 100. Se al doppio del nostro numero aggiungi la metà del nostro numero, poi aggiungi ancora un quarto del nostro numero e infine aggiungi te stessa, il risultato è 100, ma … beh si capisce”
Quante sono le oche dello stormo?
1. SOLUZIONE. Indichiamo con x il numero di oche dello stormo e avremo la seguente equazione: 2x + ½ x + ¼ x + 1 = 100. Risolvendo (16x + 4x + 2x + 1) /8 = 100 che diviene 22x = 792 infine x = 36. Lo stormo è composto da 36 oche.
L’autore propone anche una soluzione grafica mediante un immaginario dialogo tra l’oca solitaria e una saggia cicogna. “L’oca solitaria incontrò una cicogna e le raccontò l’accaduto. La cicogna tracciò una linea sulla terra con il becco per rappresentare lo stormo di oche. Poi tracciò una seconda linea della stessa lunghezza, una terza linea lunga la metà, quindi una quarta linea lunga un quarto e infine un punto, per rappresentare l’oca. Con pazienza, la cicogna spiegò il significato delle linee: le prime due rappresentavano lo stormo, la terza mezzo stormo, la quarta un quarto di stormo e il punto indicava l’oca. Poi cancellò il punto lasciando le quattro righe che rappresentavano 99 oche.
«Dato che uno stormo è composto quattro quarti, quanti quarti in tutto sono rappresentati da queste linee?»Lentamente l’oca calcolò la somma 4 + 4 + 2 + 1 e rispose: «Undici». «E se 11 quarti equivalgono a 99 oche, quante oche ci sono in un quarto di stormo?».
«Nove.»
«E allora quante nell’intero stormo?»
L’oca moltiplicò 9 x 4 e rispose: «Trentasei»
«Esatto! Ma non potevi arrivarci da sola?».
2. Cinghie e ruote. Le ruote A, B, C e D sono collegate tra loro da alcune cinghie come in figura. Se la ruota A inizia a girare in senso orario, come indica la freccia, gireranno tutte e quattro le ruote? E in caso affermativo, in quale senso girerà ciascuna di esse?
Le ruote potrebbero girare ugualmente se le quattro cinghie fossero tutte incrociate? E se a essere incrociate fossero tre cinghie? O solo una cinghia?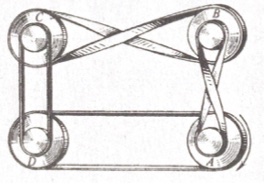
2. SOLUZIONE. Sì gireranno tutte e quattro le ruote; in particolare C e D girano in senso orario, B in senso antiorario. Le ruote girano anche se tutte e quattro le cinghie sono incrociate, ma non girano se le cinghie incrociate sono tre o solo una.
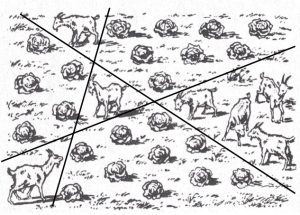
3. Capre e cavoli. Siete in grado di separare tutte le capre dai cavoli di questa figura tracciando 3 linee rette?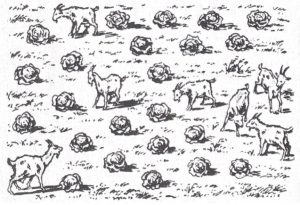
3. SOLUZIONE. Ecco come fare.
4. Il volume di una bottiglia. Siete capaci di calcolare il volume di una bottiglia, parzialmente ripiena di liquido, che ha la base rotonda, quadrata o rettangolare, ma sempre piatta, utilizzando unicamente un righello? Non potete versare il liquido né aggiungerne.
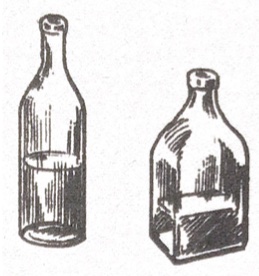4. SOLUZIONE. L’area di un quadrato, di un rettangolo o di un cerchio si può calcolare facilmente misurando i lati o il diametro con un righello. Definendo s questa area della base, con la bottiglia dritta si misura l’altezza h1 del liquido, per cui la parte piena della bottiglia avrà volume sh1. Ora capovolgendo la bottiglia, si misura l’altezza h2 dello spazio vuoto. Questo spazio della bottiglia avrà volume sh2, quindi il volume totale sarà: s(h1 + h2).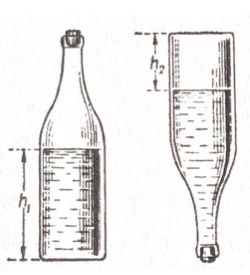
5. Sei fili d’erba. Nella Russia rurale era diffusa la pratica del seguente gioco. Una ragazza prendeva sei lunghi fili d’erba e li teneva in mano.
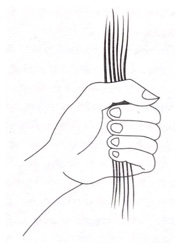
Una sua amica legava le sei estremità superiori in tre coppie, poi annodava le sei estremità inferiori formando altre tre coppie. A questo punto, la ragazza apriva il pugno e se i fili d’erba erano uniti in un unico grande anello, si diceva che si sarebbe sposata entro un anno. E’ più probabile che le venga detto che si sposerà oppure no?
5. SOLUZIONE. È più probabile che le venga detto che si sposerà. Una volta che le estremità superiori sono unite a coppie, i fili di erba possono essere disposti in questo modo.
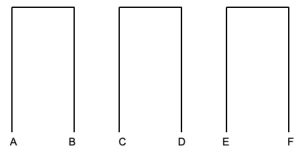
Per creare un anello unico, l’estremità A può essere unita a qualsiasi estremità eccetto B, ciò significa che ci sono è 4 opzioni possibili su 5. Una volta che A è unito a un’estremità consentita, ipotizziamo C, allora B può unirsi a qualsiasi punto tranne D, poiché questo chiuderebbe un anello di quattro fili d’erba. Ci sono quindi 2 opzioni su 3 per B. Ipotizziamo che B venga unito con E. A questo punto la coppia deve essere F e D. In altri termini la probabilità di creare un anello unico sono 4/5 * 2/3 = 8/15, poco più della metà. Per completare il quadro, sono possibili altri due risultati: tre anelli piccoli; due anelli grandi e uno piccolo. Le probabilità sono rispettivamente 1/15 e 6/15.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
8 risposte
Sì, penso che sia proprio così.
Riferito a: ” L’oca solitaria è funzionale alla costruzione dell’equazione ma non fa parte dello stormo.”
Segnalo due interessanti commenti, che sono arrivati simultaneamente, a integrazione e completamento della soluzione al problema n. 5.
Giuseppe Costanzo: “Si può generalizzare al caso con n fili con il semi-fattoriale : (n-2)!!/(n-1)!!”.
Giorgio Vecchi: “Si può scrivere la formula generale per n (pari) utilizzando il fattoriale doppio (!!). p = (n – 2)!! / (n – 1)!!”
Infatti, applicando al nostro problema avremo (2 * 4) / (1 * 3 * 5) = 8/15.
Grazie per la collaborazione
Lo stormo non è composto da 36 oche, perchè nelle 36 oche c’è pure quella (contata con “e infine aggiungi te stessa”) l’oca SOLITARIA: “Un’oca solitaria stava volando in direzione opposta a uno stormo di oche”.
Dunque 36 – 1 = 35.
O forse no? Perchè facendo la “prova” i conti non tornano (e neanche le oche tornano).
Però… se son 36, dov’è il trabocchetto? E’ una semplice equazione (che io son riuscito a sbagliare…).
Se ci atteniamo al testo, viene chiesto il numero delle oche dello stormo, come indicato dall’autore Boris Kordemsky.
Appunto, “Un’oca solitaria stava volando in direzione opposta”: SOLITARIA e DIREZIONE OPPOSTA evidenziano che l’oca in questione è fuori dalla stormo.
Quindi dove dice: “e infine aggiungi te stessa” va bene per l’equazione, ma alla fine devi TOGLIERE “te stessa” in quanto non facente parte dello stormo.
36 è il risultato dell’equazione, 35 oche nello stormo + 1 oca solitaria che va in senso opposto.
O no?
Continuo a pensare che lo stormo sia di 36 oche e, con quella solitaria e in direzione opposta, avremo in totale 37 oche. L’oca solitaria è funzionale alla costruzione dell’equazione ma non fa parte dello stormo.