
I Giochi del Lunedì di Prisma del 21 marzo 2022 a cura di Fabio Ciuffoli
Oggi proponiamo quattro problemi tratti da Gli Enigmi di Mosca di Boris Kordemsky, uno dei più apprezzati e popolari libri di giochi matematici, best seller europeo e internazionale e probabilmente il libro del genere più diffuso da sempre. Il divulgatore americano Martin Gardner ha adattato con successo il testo ai canoni occidentali ed è inoltre l’autore del quinto gioco. Invitiamo i lettori a inviarci osservazioni e proposte di soluzioni nello spazio riservato ai commenti. Domani pomeriggio alle 17.00 publicheremo le soluzioni.
Gli enigmi di Mosca
1. L’indovinello dell’oca. Un’oca solitaria stava volando in direzione opposta a uno stormo di oche. Passando gridò: “Salve, 100 oche!”. L’oca che era a capo dello stormo le rispose: “Noi non siamo 100. Se al doppio del nostro numero aggiungi la metà del nostro numero, poi aggiungi ancora un quarto del nostro numero e infine aggiungi te stessa, il risultato è 100, ma … beh si capisce”
Quante sono le oche dello stormo?
2. Cinghie e ruote. Le ruote A, B, C e D sono collegate tra loro da alcune cinghie come in figura. Se la ruota A inizia a girare in senso orario, come indica la freccia, gireranno tutte e quattro le ruote? E in caso affermativo, in quale senso girerà ciascuna di esse?
Le ruote potrebbero girare ugualmente se le quattro cinghie fossero tutte incrociate? E se a essere incrociate fossero tre cinghie? O solo una cinghia?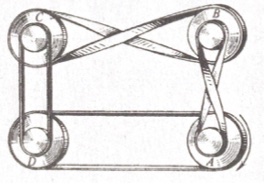
3. Capre e cavoli. Siete in grado di separare tutte le capre dai cavoli di questa figura tracciando 3 linee rette?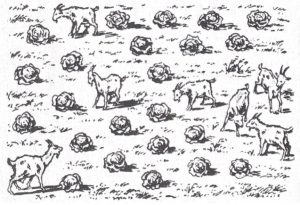
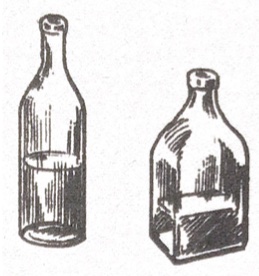
4. Il volume di una bottiglia. Siete capaci di calcolare il volume di una bottiglia, parzialmente ripiena di liquido, che ha la base rotonda, quadrata o rettangolare, ma sempre piatta, utilizzando unicamente un righello? Non potete versare il liquido né aggiungerne.
5. Sei fili d’erba. Nella Russia rurale era diffusa la pratica del seguente gioco. Una ragazza prendeva sei lunghi fili d’erba e li teneva in mano.
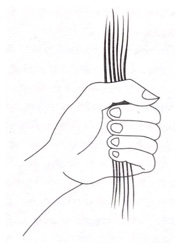
Una sua amica legava le sei estremità superiori in tre coppie, poi annodava le sei estremità inferiori formando altre tre coppie. A questo punto, la ragazza apriva il pugno e se i fili d’erba erano uniti in un unico grande anello, si diceva che si sarebbe sposata entro un anno. E’ più probabile che le venga detto che si sposerà oppure no?
Aggiornamento per le soluzioni click qui
I giochi 1, 2, 3 e 4 sono tratti da “Gli enigmi di Mosca di Boris A. Kordemsky. Il gioco 5 è una rielaborazione da Martin Gardner “Tying the Grass and Tying the Knot”.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
10 risposte
1) 35
2) A, B, C, in senso antiorario, D orario
3) Vedi immagine (segmenti con tratto spesso, fosse stato più leggero non avrei dovuto limare qualche corna di capra).
4) Con le formule, assumendo il vetro di spessore trascurabile e considerando “solido” da misurare il cilindro, o parallelepipedo formato dall’acqua (o liquido).
Cilindro: misuro il diametro base e altezza colonna di liquido. V = hπr^2, parallelepipedo di base a x b e altezza (del liquido sempre) c: V = abc.
5) A spanne 8/15: le tre coppie da sotto van comunque bene; prima coppia sopra ha 4/5 di probabilità; in caso positivo la seconda ha probabilità 2/3 e la terza è obbligata. 4/5 x 2/3 = 8/15 > 1/2. E’ più probabile che si sposerà entro l’anno, o meglio, che il gioco affermi ciò.
Ops, il volume DELLA BOTTIGLIA, non del liquido.
Allora… mumble mumble, ci penso…
OK, misuro come detto sopra il volume del liquido.
Poi capovolgo la bottiglia e misuro con lo stesso metodo il volume dell’aria.
Infine addiziono i due volumi.
Non è proprio 35… ottime le altre soluzioni. A domani per tutte le soluzioni con dimostrazione.
1. 36
2.a Girano tutte e 4 le ruote, B in senso antiorario, C e D in senso orario
2.b Con 4 cinghie incrociate le ruote girerebbero, con 1 o 3 no
3. Vedi immagine allegata
4. Si calcola il volume della parte di bottiglia fino al livello del liquido, che è un cilindro o un parallelepipedo; dopodichè si ribalta la bottiglia e si calcola il volume della parte vuota, che è sempre un cilindro o un parallelepipedo; infine si sommano i due volumi che daranno il volume totale della bottiglia
5. Annodate le estremità superiori si ottengono tre fili d’erba con 6 estremità A B C D E F. Le possibilità di annodare queste sei estremità a 2 a 2 sono 15, di cui 8 formano un unico anello e 7 no.
AB CD EF no
AB CE DF no
AB CF DE no
AC BD EF no
AC BE DF si
AC BF DE si
AD BC EF no
AD BE CF si
AD BF CE si
AE BC DF si
AE BD CF si
AE BF CD no
AF BC DE si
AF BD CE si
AF BE CD no
Perfetto. A domani per le soluzioni.
Il quesito 5 mi sembra il più divertente, penso che lo proporrò quando capiterà ai miei studenti, sempre che io stesso abbia capito la soluzione!
Una volta legati i capi superiori dei fili d’erba scelgo un capo inferiore e lo lego a uno degli altri 5. In un caso su 5 l’avrò legato al filo che è già connesso superiormente e quindi non si può più ottenere un’unica catena mentre negli altri 4 casi è possibile. I quattro capi rimasti liberi si possono legare in 3 modi diversi (per il primo che scelgo ho 3 possibilità e gli ultimi due capi vengono legati per forza tra loro). Solo in un caso su 3 lego inferiormente due fili della stessa copia connessa già superiormente ma non ancora utilizzata inferiormente (2 casi su tre danno un unico grande anello). Per le probabilità composte 4/5 x 2/3= 8/15 che è leggermente superiore al 53% per cui è più probabile le venga detto che si sposerà!
Grazie per tutti gli stimoli settimanali!
Perfetto e grazie per la partecipazione. A domani per le altre soluzioni.
1) Se imposto l’equazione :
2x +1/2× +1/4× + 1 =100…l’incognita vale 36.
4) Se immagino la bottiglia divisa in 3 parti…il corpo centrale..il restringimento..il collo..applicando le regole per calcolare i vari volumi e sommandoli…ottengo il volume totale.
Ottima la risposta al primo problema. A domani per tutte le altre soluzioni.