
Le soluzioni del 7 marzo 2022 a cura di Fabio Ciuffoli
Nella mattinata di ieri abbiamo proposto tre giochi a supporto del XXIX Congresso Internazionale dei Matematici (ICM) in programma per luglio 2022. Di seguito presentiamo le soluzioni con dimostrazione.
Congresso Internazionale dei Matematici – soluzione
1. Scambio di animali domestici. Un gatto è seduto sul tavolo e una tartaruga sta camminando sul pavimento proprio sotto il gatto. La distanza dalle orecchie del gatto alla sommità del guscio della tartaruga è di 170 cm. Alena ha cambiato la posizione dei suoi animali domestici. Ora la distanza dalle orecchie del gatto alla parte superiore del guscio della tartaruga è di 130 cm. Qual è l’altezza del tavolo?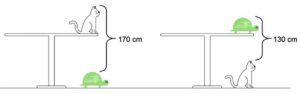
2. SOLUZIONE. Mettiamo il tavolo della prima immagine sul tavolo della seconda immagine, in modo che le tartarughe siano allineate.
La distanza dalle orecchie del gatto in basso alle orecchie del gatto in alto sarà 130 + 170 = 300 cm. Questa distanza è pari al doppio dell’altezza del tavolo, quindi la risposta è 150 cm.
In alternativa, indicando con X l’altezza del tavolo, con G l’altezza del gatto e con T l’altezza della tartaruga, si può impostare il seguente sistema:
Riducendo avremo 2X = 300 quindi X = 150 cm.
2. Pensiero circolare. Volodya sta correndo su una pista circolare a velocità costante. Sulla pista sono stati collocati due segnali gialli. All’inizio della corsa, Volodya è stato più vicino al primo segnale giallo per 2 minuti, poi è stato più vicino al secondo segnale giallo per 3 minuti, e successivamente è stato di nuovo più vicino al primo segnale giallo. Quanto tempo impiega Volodya a fare un giro completo?
2. SOLUZIONE. Indichiamo il primo e il secondo segnale con A e B. Dal punto intermedio C, tracciamo il diametro in modo che ogni punto su CD sia equidistante da A e B. Abbiamo così due semicirconferenze, dove tutti i punti di una semicirconferenza sono più vicini ad A e tutti i punti dell’altra sono più vicini a B.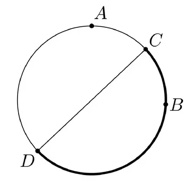
Se Volodya è più vicino a B per 3 minuti, significa che percorre l’arco CBD in 3 minuti e di conseguenza, percorre l’intera circonferenza in 6 minuti. Il dato che Volodya è stato più vicino al primo segnale giallo per i primi 2 minuti, non è necessario per determinare il tempo in cui esegue un giro completo.
3. Via per la gloria. Olga deve percorrere l’area 3 x 3 in basso a sinistra, muovendosi orizzontalmente o verticalmente da una cella all’altra, senza entrare nella stessa cella più di una volta. In basso a destra viene mostrato l’esempio di un possibile percorso. Se Olga annota le cifre, in ordine durante questo percorso, otterrà il numero 84937561. Qual è il numero più grande che Olga può ottenere durante un percorso attraverso la griglia?
3. SOLUZIONE. Innanzitutto, consideriamo che un numero di nove cifre è più grande di un numero con meno cifre e perciò Olga cercherà di attraversare tutte le celle. Successivamente, è ovvio che il numero più alto è quello che inizia con la cifra più alta. 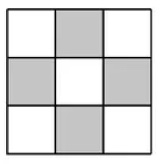
Ora, colorando la scacchiera come mostrato a destra, durante il cammino il colore delle celle deve alternarsi e poiché ci sono cinque celle bianche e quattro celle nere, è conveniente iniziare con una cella bianca. Il numero più grande nelle celle bianche è 5.
In seguito, ad ogni passaggio è necessario massimizzare la cifra successiva, ovvero andare alla cella con la cifra più grande possibile e perciò Olga andrà sul 7 e poi sul 3. Il numero massimo, tra i vicini del numero 3, è 9, ma se Olga andasse sulla cella 9, non sarebbe in grado di completare il percorso e la griglia si spezzerebbe in due aree non collegate. Non può andare da 3 a 8 per lo stesso motivo, quindi va alla cella 6. A questo punto la via da seguire è inequivocabile: 573618492.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
Una risposta
Allego l’immagine proposta da Massimo Molinelli per illustrare, senza parole, la soluzione al gioco n. 3. Grazie per la collaborazione.