
I Giochi del lunedì di Prisma del 7 marzo 2022 a cura di Fabio Ciuffoli
Il Congresso Internazionale dei Matematici (ICM) in programma per il prossimo luglio, non si svolgerà nella sede prevista di San Pietroburgo, ma esclusivamente on line. Alla luce della situazione in Ucraina e dopo la pressione delle società matematiche nazionali, l’Unione Matematica Internazionale (IMU) ha comunicato che l’evento sarà interamente virtuale. E’ un incontro quadriennale, con la partecipazione di circa 5.000 matematici provenienti da tutto il mondo, durante il quale si assegnano i premi più importanti tra cui il prestigioso Medaglia Fields. Per promuovere l’evento, è stato organizzato un concorso di matematica online per studenti e pubblico in generale. Di seguito proponiamo le prime tre domande, che mettono alla prova il ragionamento logico e le abilità matematiche.
Congresso Internazionale dei Matematici
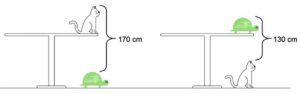
1. Scambio di animali domestici. Un gatto è seduto sul tavolo e una tartaruga sta camminando sul pavimento proprio sotto il gatto. La distanza dalle orecchie del gatto alla sommità del guscio della tartaruga è di 170 cm. Alena ha cambiato la posizione dei suoi animali domestici. Ora la distanza dalle orecchie del gatto alla parte superiore del guscio della tartaruga è di 130 cm. Qual è l’altezza del tavolo?
2. Pensiero circolare. Volodya sta correndo su una pista circolare a velocità costante. Sulla pista sono stati collocati due segnali gialli. All’inizio della corsa, Volodya è stato più vicino al primo segnale giallo per 2 minuti, poi è stato più vicino al secondo segnale giallo per 3 minuti, e successivamente è stato di nuovo più vicino al primo segnale giallo. Quanto tempo impiega Volodya a fare un giro completo?
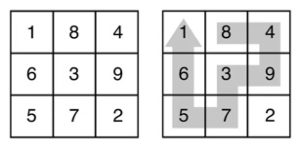
3. Via per la gloria. Olga deve percorrere l’area 3 x 3 in basso a sinistra, muovendosi orizzontalmente o verticalmente da una cella all’altra, senza entrare nella stessa cella più di una volta. In basso a destra viene mostrato un possibile percorso. Se Olga annota le cifre, in ordine durante questo percorso, otterrà il numero 84937561. Qual è il numero più grande che Olga può ottenere durante un percorso attraverso la griglia?
 Aggiornamento per le soluzioni click qui
Aggiornamento per le soluzioni click qui
I giochi fanno parte di una prova predisposta dall’ICM.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
15 risposte
1)
T + x – y = 170
T – x + y = 130
Sommo: 2T = 300
T = 150
2) 2′ + 2′ + 1′ + 1′ = 6′
3) Per avere il massimo numero conviene sfruttare tutte le cifre.
Per sfruttarle tutte devo partire da un angolo, dunque scelgo quello col n° maggiore: 5:
573618492.
Perfetto. Trovi le soluzioni al link sopra “click qui”.
Colgo l’occasione per fare una domanda, dato che il congresso si terrà online, sarà aperto a tutti gli interessati o riservato ai matematici invitati?
Tutte le informazioni si trovano al link dell’International Mathematical Union (IMU) che organizza il congresso.
https://www.mathunion.org
1) Ragionando con la vista
85 + 65 =150 cm
3) 573618492
Ottimo a domani per tutte le soluzioni.
1) 150 cm
2) 6 minuti (S1—->2’+2′ S2 —->1’+1’S1)
3) 5 7 3 6 1 8 4 9 2
Ottimo, a domani per le soluzioni con dimostrazione.
Quesito 3: il numero più grande che può ottenere è 94.837.561. Affinché il numero sia il più grande possibile, per ogni cifra bisogna scegliere la possibilità maggiore partendo ovviamente dal 9.
C’è un modo per utilizzare tutte e nove le cifre e ottenere così un importo di centinaia di milioni.
Sì, grazie per la correzione
La situazione può essere schematizzata in questo modo. In ordine alfabetico denominiamo i punti evidenziati nell’immagine: A il punto di partenza, B il primo segnale giallo, C il primo punto azzurro, D il secondo segnale giallo ed E il secondo punto azzurro. Superato un punto azzurro, passa dalla situazione in cui è più vicino ad un segnale alla situazione in cui è più vicino all’altro. Una volta raggiunto il primo segnale, continua ad essere più vicino ad esso di un arco BC in modo che percorra AC in 2 minuti; superato C inizia ad essere più vicino al secondo segnale D: questo significa che DC è uguale a BC. Per lo stesso motivo di simmetria, E si trova a metà dell’arco DB, dato che una volta superato si trova di nuovo più vicino al primo segnale. CE è quindi una semicirconferenza che percorre in 3 minuti. Dato che percorrerebbe EC nello stesso tempo è percorre AC in 2 minuti, allora percorre EA in 1 minuto (si muove a velocità costante). Perciò impiega 6 minuti per un giro completo.
Perfetto.
Quesito 1: chiamiamo G l’altezza del gatto, H l’altezza del tavolo e T l’altezza della tartaruga. Abbiamo allora il sistema
G+H-T=170 cm
T+H-G=130 cm.
Sommando le due equazioni notiamo che si semplificano G e T, abbiamo perciò un’equazione di primo grado in H:
2H=300 cm -> H=150 cm.
Ottimo, a domani per tutte le soluzioni.