
Le soluzioni del 15 novembre 2021 a cura di Fabio Ciuffoli
Ieri mattina abbiamo proposto quattro problemi, collegati al mese di novembre, ora presentiamo le soluzioni con le relative dimostrazioni.
Olio, vino e black friday – soluzioni
1. Un commerciante ha acquistato alcuni maglioni dal costo unitario di 100 euro che mette in vendita, normalmente, con un ricarico dell’80% sul costo, quindi ricavando 180 euro. Nella vendita straordinaria del Black Friday, quale sconto percentuale, sul prezzo di vendita, può concedere se vuole ottenere un guadagno di 15 euro? [Si tralasciano per semplicità l’incidenza delle spese generali e altri elementi accessori]
1. SOLUZIONE. Il ricavo, in condizioni normali, è 180 euro e il guadagno è 80 euro. Se il commerciante vuole ottenere un guadagno di 15 euro, dovrà vendere un maglione a 115 euro, quindi con uno sconto di 65 euro. La percentuale di sconto sarà (65/180) * 100 = 36%.
2. Dieci persone impiegano, lavorando allo stesso ritmo, quattro giorni per raccogliere 8 tonnellate di olive. Sapendo che 1 quintale di olive rende mediamente 16 kg di olio, quanti giorni dovrebbero lavorare due persone per assicurare kg 320 di olio?
2. SOLUZIONE. Il problema si può risolvere in diversi modi. Dieci persone che lavorano per 4 giorni corrispondono al 40 giorni lavoro-persona. Allora in un giorno lavoro-persona si raccoglieranno 8.000/40 = 200 kg di olive. In un giorno, 2 persone raccoglieranno 400 kg di olive, che produrranno 4*16 = 64 kg di olio. Ora, quelle due persone per produrre 320 kg di olio avranno bisogno di 5 giorni (320/64 = 5g).
3. Un consumatore acquista dalla Cantina Brolli una certa quantità di litri di vino per 240 euro. Se si rivolgesse alla concorrente Enoteca Zanni pagherebbe 4 euro in più al litro e così, con la stessa cifra di 240 euro, acquisterebbe 3 litri in meno. Quanti litri ha acquistato dalla Cantina Brolli e a che prezzo al litro?
3. SOLUZIONI. Definendo L i litri e P il prezzo del vino della Cantina Brolli, si imposta il sistema di due equazioni con due incognite 
La soluzione dell’equazione di secondo grado è x₁ = 16 e x₂ = – 20. La soluzione negativa non è accettabile quindi il prezzo del vino della Cantina Brolli è 16 euro e la quantità venduta è 15 litri. Per completezza, La Cantina Zanni vende 12 litri a 20 euro al litro.
4. Marina sta vendendo porta a porta dei biglietti per una degustazione. Il prezzo è 11 euro per gli adulti e 9 euro per i ragazzi. Ha incassato in totale 124 euro. Quanti biglietti ha venduto di ragazzi e di adulti?
4. SOLUZIONE. Ci sono diversi modi per risolvere questo problema. Si imposta l’equazione A*11 + R*9 = 124 dove A rappresenta il numero di adulti e R il numero dei ragazzi, che devono essere interi. Abbiamo una equazione con due incognite e dobbiamo trovare quei numeri interi che moltiplicati per 11 e per 9 danno somma 124. In questo caso procediamo in modo empirico, ma si potrebbe anche utilizzare un grafico cartesiano o il Teorema di Bezout. In primo luogo viene escluso che siano tutti adulti o tutti ragazzi, perché 124 non è divisibile né per 9 né per 11. Possiamo costruire la tabella, con in colonna le varie ipotesi di adulti paganti, il totale pagato dagli adulti e il resto eventualmente pagato dai ragazzi.
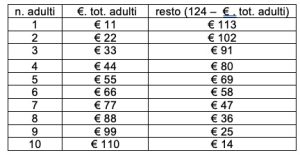
Esaminando le varie possibilità, troviamo che 36 è l’unico “resto” multiplo di 9. Quindi avremo 8 adulti paganti 11 euro ciascuno per un totale di 88 euro, con un resto di 36 euro è perciò 4 ragazzi paganti. E’ questa l’unica possibilità in quanto non vi sono altri resti divisibili per 9.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
2 risposte
Un ulteriore metodo per risolvere questo tipo di problemi prevede l’utilizzo del Teorema di Bézout.
Partiamo dalla nostra equazione: A*11 + R*9 = 124 dove A rappresenta il numero di adulti e R il numero dei ragazzi, che devono essere interi.
Iniziamo calcolando i due numeri interi, m e n, tali che
11m + 9n = 1 che saranno m = 5; n = – 6.
Ora moltiplichiamo m e n per 124:
5 * 124 = 620; – 6 * 124 = – 744.
A questo punto dobbiamo vedere per quali valori interi di h, le variabili A e R sono entrambe maggiori o uguali a zero.
A = 620 – 9h ≥ 0 da cui si ricava che h ≤ 68
R = – 744 + 11h ≥ 0 da cui si ricava che h ≥ 68
Quindi h può assumere un solo valore intero 68.
Poniamo h = 68 avremo: A = 620 – 9*68 = 8; R = – 744 + 11*68 = 4.
In sintesi, i tre metodi proposti per la soluzione: empirico tabellare, grafico e del Teorema di Bézuot si possono applicare a problemi di questo tipo. Ovviamente la scelta dipende dal grado di complessità e dal tempo a disposizione.
A integrazione della soluzione al problema 4, Marina che vende biglietti per la degustazione a adulti e ragazzi, propongo la rappresentazione su un grafico cartesiano dell’equazione A * 11 + 9 * R = 124 e individuo i punti di incontro con entrambi i valori interi (adulti 8, ragazzi 4).