
Le soluzioni del 19 luglio 2021 a cura di Fabio Ciuffoli
Vedere la geometria – soluzioni
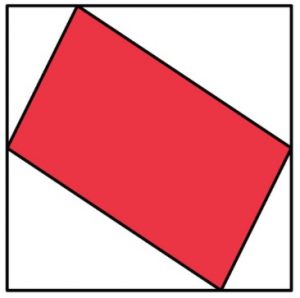
1. Un parallelogramma è inscritto in un quadrato in modo che due suoi vertici toccano il punto medio dei lati opposti. Quale frazione del quadrato è ombreggiata in rosso?
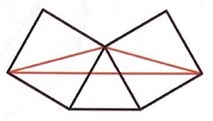
2. Il triangolo grande è equilatero. Il triangolo rosso è costruito utilizzando i punti medi dei due lati e un vertice del triangolo equilatero. Qual è il rapporto tra l’area del triangolo rosso e l’area del triangolo grande?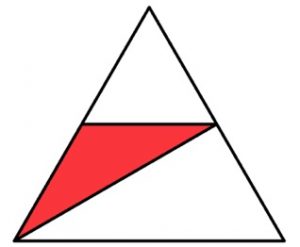
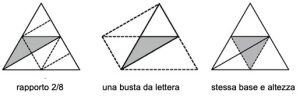
2. SOLUZIONE. Il triangolo rosso è ¼ del triangolo grande. Si può dimostrare in almeno tre modi: a) dividendo l’intero triangolo in 8 piccoli triangoli uguali e deducendo che il triangolo rosso ne comprende due, quindi 2/8 o ¼; b) disegnando una forma a “busta” che ha la stessa area del triangolo ABC e deducendo che il triangolo rosso è un quarto di questa busta; c) dividendo il triangolo ABC in quattro triangoli più piccoli uguali tra loro e deducendo che il triangolo rosso ha area uguale a uno di questi triangoli più piccoli, perché se due triangoli hanno la stessa base e altezza, hanno la stessa area.
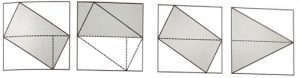
3. Per le due costruzioni di fiammiferi mostrate in figura, siete in grado di dimostrare che le linee rette, tra le teste dei fiammiferi inutilizzati sui vertici più esterni in ogni diagramma, hanno la stessa lunghezza?
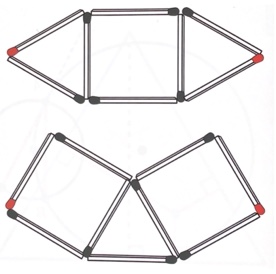
3. SOLUZIONE. Presentiamo due modi. Primo modo. Le due costruzioni possono comporre un dodecagono regolare nel quale le linee rette in questione, costituiscono i lati di un quadrato.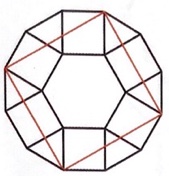
Secondo modo. Supponiamo che un fiammifero abbia una lunghezza unitaria. Per il quadrato con due triangoli equilateri, la lunghezza richiesta è il lato del quadrato più 2 volte l’altezza del triangolo:
1 + 2 * (√3/2) = 1 + √3
Per il triangolo con due quadrati, utilizziamo la regola del coseno di un triangolo isoscele con lati √ 2 e angolo maggiore 45 + 60 + 45 = 150 e quindi 180 – 150 = 30.
Definendo x la base avremo: x2 = 4[1 + cos(30)] = 4 + 2√3 = (1 + √3)² e infine x = 1 + √3.
Un problema, relativo ad una costruzione simile, è stato proposto nelle Prove INVALSI del 2011 per le classi terze medie. Riportiamo di seguito il testo con le soluzioni.
Il pavimento di un’antica casa romana, riprodotto con a fianco la sua schematizzazione geometrica, presenta un dodecagono composto da un esagono regolare interno, sei quadrati uguali e sei triangoli equilateri uguali.
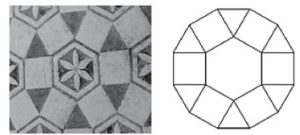
Indicare se le seguenti affermazioni sono vere o false.
a. L’area dell’esagono è metà dell’area del dodecagono?
b. L’area di ciascun triangolo è un sesto dell’area dell’esagono?
c. L’area di un quadrato è il doppio dell’area di un triangolo?
d. Il perimetro del dodecagono è il doppio di quello dell’esagono?
SOLUZIONI
a. Falso. L’area dell’esagono regolare è l² * 2,598, dove l è il lato. Il dodecagono contiene 6 quadrati di area l² * 6 più 6 triangoli equilateri di lato l. Quindi la sola l’area dei quadrati supera il doppio dell’area dell’esagono, per cui l’area del dodecagono è di gran lunga maggiore del doppio dell’area dell’esagono.
b. Vero. Si può osservare che l’esagono si compone esattamente di 6 triangoli equilateri di lato l.
c. Falso. Il triangolo equilatero ha la stessa base del quadrato ma ha altezza inferiore al lato del quadrato.
d. Vero. L’esagono ha sei lati di misura l e il dodecagono ha 12 lati di misura l.
A lunedì prossimo
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
3 risposte
Una soluzione alternativa (senza formule) al terzo quesito.
Considero i due quadrilateri formati (nelle due costruzioni) dai tre fiammiferi “più in basso” e che hanno come quarto lato i due segmenti che occorre dimostrare essere uguali. Gli angoli corrispondenti di questi quadrilateri sono uguali fra loro (due perché di 90 +60 gradi, in entrambe le costruzioni; gli altri due perché, in entrambe le costruzioni, per simmetria, la metà di 60 gradi). Quindi anche gli altri due lati sono uguali fra loro. Fine.
Si può anche immaginare di costruire un meccanismo articolato con tre bacchette incernierate fra loro e di uguale lunghezza: una volta che siano fissati i due angoli fra queste bacchette (150 gradi) il meccanismo diventa rigido, e di conseguenza risulta fissata anche la distanza fra i due estremi. Fine.
Ottima alternativa, hai “fatto vedere” due trapezi congruenti, quindi con uguale base maggiore, non facili da vedere prima della descrizione.
Dopo aver visto le soluzioni, facile grazie anche alle immagini, mentre difficile descrivere le soluzioni senza ausilio di immagini. Comunque bellissime soluzioni senza formule!