I giochi del lunedì di Prisma 19 luglio 2021 a cura di Fabio Ciuffoli
Presentiamo tre problemi sotto forma di giochi e invitiamo i lettori a proporre osservazioni e soluzioni nello spazio riservato ai commenti. Alle ore 17.00 di domani publicheremo le soluzioni.
Vedere la geometria
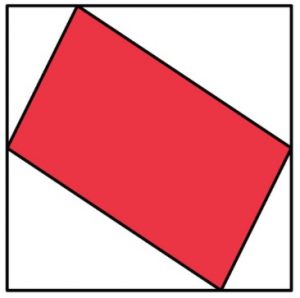
1. Un parallelogramma è inscritto in un quadrato in modo che due suoi vertici toccano il punto medio dei lati opposti. Quale frazione del quadrato è ombreggiata in rosso?
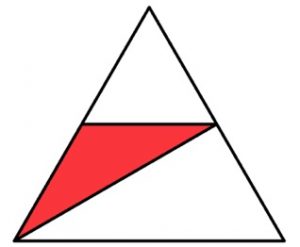
2. Il triangolo grande è equilatero. Il triangolo rosso è costruito utilizzando i punti medi dei due lati e un vertice del triangolo equilatero. Qual è il rapporto tra l’area del triangolo rosso e l’area del triangolo grande?
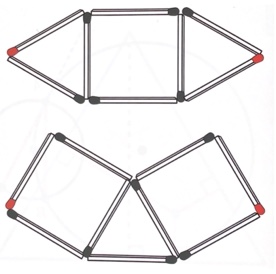
3. Siete in grado di dimostrare che, nelle due costruzioni di fiammiferi, le linee rette, tra le teste dei fiammiferi inutilizzati sui vertici più esterni, hanno la stessa lunghezza?
 Aggiornamento per le soluzioni click qui
Aggiornamento per le soluzioni click qui
I giochi di oggi sono rielaborazioni tratte da Geometry snacks di E. Southall – V. Pantaleoni.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
11 risposte
1) Se tracciamo una linea immaginaria che unisce i due vertici che toccano il punto medio dei due lati e prendiamo in considerazione solo una delle due metà divise dalla linea immaginaria vediamo un triangolo rettangolo (quello rosso) e altri due triangoli più piccoli… se uniamo l’altezza del triangolo bianco di destra con quella del triangolo bianco di sinistra otteniamo un ulteriore triangolo rettangolo congruente al primo (se capovolto). Se ripetiamo la stessa procedura anche nell’altra metà troveremo due triangoli rettangoli rossi e due bianchi. Quindi in conclusione possiamo dire che la metà del quadrato è rossa mentre la restante metà è bianca; sotto forma di frazione 1/2.
2) In questo quesito dobbiamo dividere il triangolo in altri quattro triangoli più piccoli che chiameremo T, li otteniamo unendo tutti i punti medi del triangolo grande. Ora abbiamo il triangolo rosso che occupa due triangoli T se idealmente uniamo le due parti rosse ricaviamo un unico triangolo T rosso. Quindi troveremo tre triangoli bianchi e uno rosso che in frazione viene espresso come 1/4.
3) Per dimostrare che hanno lunghezza uguale le due rette che collegano le teste rosse dei fiammiferi dobbiamo contare il numero di parti delle due figure: nella prima figura possiamo contare un fiammifero (il lato del quadrato) più due altezze dei triangoli ai lati; nella seconda figura contiamo un fiammifero (il lato del triangolo) e poi se trasliamo il triangolo della figura superiore a quella inferiore seguendo una retta perpendicolare a quella delle teste dei fiammiferi noteremo che il vertice del triangolo traslato coincide con il vertice del triangolo della figura inferiore. Se facciamo la stessa cosa anche dall’altro lato possiamo dimostrare che le lunghezza della retta superiore che unisce i due fiammiferi rossi è uguale a quella della retta inferiore.
Il primo è 1/2 facile
Il secondo difficoltà media 1/4
Il terzo non vedo la soluzione al momento
1: E’ la metà. Se tracciamo un linea tra i 2 punti mediani dividiamo in 2 il parallelogramma dividendo la zona rossa in 2 triangoli equivalenti. Se poi tracciamo l’altezza dei 2 triangoli osserviamo che i lati sono la diagonale di altri parallelogrammi e pertanto la zona rossa è la metà dell’area totale.
2: Anche qui se congiungiamo i punti medi dei lati con il punto medio della base otteniamo 4 triangoli equilateri equivalenti tra loro e la zona rosssa interessa la metà di 2 di questi. Pertanto la zona rosssa è un quarto del totale.
3: Nella prima figura la retta che congiunge i vertici più estremi è pari ad un fiammifero più 2 volte l’altezza dei triangoli equilateri. Nella seconda figura se costruiamo idealmente 2 triangoli equilateri alla base dei 2 quadrati osserviamo che anche in questo caso la distanza tra i vertici estremi è di un fiammifero più 2 volte l’altezza dei triangoli equilateri.
PS: Certo che con la sola descrizione testuale è piuttosto difficile spiegare le soluzioni!
Bellissima la soluzione.
Forse si potrebbe descrivere più semplicemente a parole proiettando ortogonalmente i vertici della base del triangolo equilatero sul segmento di cui si sta cercando la lunghezza.
Effettivamente con un disegno la spiegazione sarebbe molto più efficace. Se vuole puó inviarmi l’immagine per email per eventualmente inserirla nelle soluzioni che verranno pubblicate domani. Nelle soluzioni è previsto l’utilizzo di immagini.
Il parallelogramma ha un’area di 1/2 di quella del quadrato. Tutti i triangoli inscritti in un rettangolo che abbiano la base coincidente con un lato del rettangolo e ed il vertice opposto alla base sul lato opposto del rettangolo avranno tutti la stessa area equivalente a metà dell’area del rettangolo. Con facile ragionamento si evince che il parallelogramma, essendo composto da due triangoli equivalenti tra loro e di area uguale a metà del rettangolo che a sua volta è metà del quadrato, avrà l’area uguale a metà di quella del quadrato.
Il triangolo rosso ha un area di 1/4 di quella del triangolo grande. Unendo i punti medi dei lati di un triangolo equilatero si ottengono 4 triangoli uguali ed equilateri a loro volta, la cui area sarà quindi 1/4 dell’area del triangolo che li contiene. Il triangolo rosso essendo formato da due metà esatte di questi triangoli equilateri, ha area equivalente anch’esso ad 1/4 del triangolo grande.
Il segmento che unisce le teste rosse dei fiammiferi è uguale nelle due figure. Se chiamiamo L la lunghezza del fiammifero e H l’altezza del triangolo equilatero di lato L, in entrambi i casi il segmento in questione sarà uguale a L + 2H
1. 1/2
2. Il triangolo rosso e quello equilatero piccolo rappresentano la metà dell’equilatero grande. Il triangolo piccolo è equilatero con i lati e altezza1/2 di quelli del triangolo grande. Esso pertanto ha estensione di rispetto al triangolo grande1/4. A questo punto il triangolo rosso risulta equiesteso con il triangolo equilatero piccolo
3. Le rette sono infinite. È forse necessario dire qualcosa sull’allineamento delle teste dei fiammiferi?
Il terzo problema chiede di dimostrare che la lunghezza del segmento che collega le due estremità (teste rosse dei fiammiferi) è la stessa, per entrambe le composizioni.
Allora il primo è facile; il secondo si può svolgere con un disegno o più disegni; il terzo è più difficile ci devo pensare e provare
1: è ombreggiato in rosso mezzo quadrato
2: il triangolino equivale ad un quarto del triangolo grande
3: le linee rette hanno la stessa lunghezza, perché sono entrambe infinite.
A domani per le soluzioni argomentate.