19. Soluzioni del 15 novembre 2021 – Il compito di selezione

Le soluzioni del 15 novembre 2021 a cura di Fabio Ciuffoli

Ieri mattina abbiamo proposto tre giochi logici sul compito di selezione e ora presentiamo le soluzioni argomentate. 

Il compito di selezione – soluzioni 

1. Quattro carte, che riportano su entrambi i lati una lettera dell’alfabeto, sono disposte nel seguente modo. Quante carte occorre girare per verificare l’affermazione: “Dietro ogni G si trova una L”?

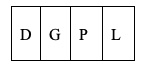
1. SOLUZIONE. Le carte da girare sono tre: G, D e P. Affinché l’affermazione sia vera, dietro G ci deve essere L, mentre dietro D e P non ci deve essere G. Non occorre girare la carta L, perché la lettera sul retro di questa carta, sia una G o no, non cambia la validità dell’affermazione.

2. Sei carte, ciascuna delle quali su un lato porta scritto una fra le lettere A, B, C e sull’altro porta scritto una fra le cifre 1, 2, 3, vengono disposte su un tavolo in questo modo.

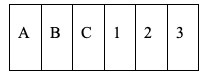Quali carte è necessario girare per determinare la verità dell’affermazione: “Se una carta porta la lettera B su un lato, allora sull’altro lato porta la cifra 2”?

2. SOLUZIONE. Le carte da girare sono: B, 1 e 3. Affinché l’affermazione sia vera, la carta B deve riportare 2, mentre la 1 e la 3 non devono riportare B. Non è necessario girare la carta 2 perché la lettera sul retro, che sia A o B o C, non cambia la validità dell’affermazione. Il problema è simile al precedente, anche in questo caso occorre chiedersi che tipo di carta potrebbe dimostrare la non verità dell’affermazione.

3. In un mazzo di carte, su ogni carta sono segnati due numeri, uno su ogni faccia e dietro ogni numero pari c’è un multiplo di 3. Quale di queste 5 affermazioni è vera?

A) una carta può contenere 3 su un lato e 5 sull’altro;

B) nessuna carta può avere su un lato un numero doppio di quello che c’è sul lato opposto;

C) se su un lato c’è 15, sull’altro lato non ci può essere 7;

D) nessuna carta può avere lo stesso numero su entrambi i lati;

E) ci può essere una carta che contiene 11 su un lato 18 sull’altro.

3. SOLUZIONE. A è vera, perché 3 o un suo multiplo può trovarsi anche dietro un numero dispari; B è falsa perché, ad esempio, 6 può avere 12 dall’altra parte; C è falsa perché un multiplo di 3 può trovarsi anche dietro un numero dispari (considerazione simile a quella del punto A); D è falsa perché un multiplo di 3 può essere anche pari ad esempio la carta può avere 6 da un lato e 6 dall’altro; E è falsa perché 18 è pari e deve avere dall’altra parte un multiplo di 3.

Riportiamo, in sintesi, l’esperimento dello psicologo Peter Wason del 1966 e replicato più volte in anni recenti. Egli ha mostrato ai partecipanti quattro carte con i simboli A, D, 3 e 7 e ha detto loro che ciascuna carta aveva un numero su lato e una lettera sull’altro.

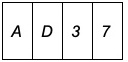Fig. 1 

Ha quindi chiesto quale delle quattro carte fosse necessario girare per verificare la regola: “Se una carta ha una A su un lato, allora ha un 3 sull’altro”. Quasi tutti i soggetti hanno scelto la A e la 3, mentre la risposta esatta è A e 7. Meno del 10% ha risposto correttamente. La maggior parte dei soggetti ha scelto la carta 3 sbagliando, infatti anche se ci fosse una lettera diversa dalla A sull’altro lato, la regola sarebbe ugualmente verificata. Invece, girando la carta 7 e non trovando una A, la regola sarebbe verificata o al contrario, trovando la A, sarebbe non verificata.

Wason ha dimostrato anche che lo stesso problema, in contesti più pratici, appare molto più semplice. Ad esempio se dovete verificare la regola: “Solo i maggiorenni possono bere alcolici” e vi trovate in un pub con quattro ragazzi: il primo ha 19 anni; il secondo vuole un’aranciata; il terzo vuole gin ed il quarto ha 15 anni, quali controllereste?  La situazione si può schematizzare e ricondurre al nostro problema: 19 anni; Aranciata; Gin e 15 anni. Quali carte controllereste per verificare la regola “Se 18 o più anni, allora può bere alcolici”?

 Ovviamente: il primo ha 19 anni e non va controllato; il secondo beve aranciata e non va controllato; il terzo ha chiesto gin e va controllato, così come il quarto che ha 15 e non può bere alcolici

 Ora che siete allenati, provate a rispondere alla seguente domanda: quali carte occorre girare, tra quelle illustrate precedentemente in figura 1, per verificare questa regola: “Se una carta ha un 3 su un lato, allora ha una A sull’altro”? [Soluzione in fondo a sinistra] 

[Soluzione la 3 e la D]

I problemi di oggi sono rielaborazioni aggiornate del Card Test presentato in Reasoning – New horizons in psychology di Peter Cathcart Wason.