
I giochi del lunedì di Prisma dell’1 novembre 2021 a cura di Fabio Ciuffoli
Wasan è una matematica partecipativa e divertente, praticata in Giappone, per risolvere problemi reali o anche per semplice divertimento. I due giochi che proponiamo oggi prendono spunto dalla matematica Wasan. Invitiamo i lettori a presentare osservazioni e proposte di soluzione nello spazio riservato ai commenti. Alle ore 17.00 di domani pubblicheremo le soluzioni.
Wasan l’arte dei numeri giapponese
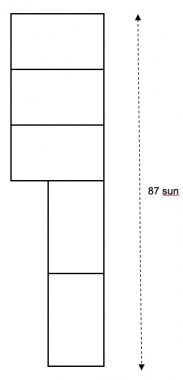
1. Sono stati preparati cinque dolci di riso noshimochi uguali a forma rettangolare. Tre vengono disposti orizzontalmente e due verticalmente, come in figura. La somma dei lati a destra è 87 sun. Sapendo che il lato lungo di ogni dolce è 21 sun, determinare la lunghezza del lato corto. (Il sun è un’unità di misura giapponese che corrisponde a 3 cm circa).
2. Durante le feste di shogatsu, il capodanno giapponese, i bambini giocano facendo rimbalzare le sfere temari. Al primo tentativo la temari viene fatta rimbalzare 9 volte. Al secondo tentativo, 23 volte. Al terzo tentativo, 45 volte e al quarto, 75 volte. Se il numero dei rimbalzi continua a crescere con questo ritmo, qual è il numero dei rimbalzi all’ottavo tentativo? Inoltre quanti tentativi sono necessari per arrivare a 423 rimbalzi?
Aggiornamento per le soluzioni click qui
I giochi proposti oggi sono tratti e rielaborati dal libro Wasan di Toshimitsu Hirano.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
16 risposte
sono d’accordo con Andrea Cravero
Per il secondo quesito ho ricercato la funzione che lega il numero di step (n) al numero di rimbalzi f(n). Con qualche difficoltà sono arrivato a trovare f(n) = 4n^2 +2n +3. Anch’io mi ero accorto che f(n+1)-f(n) era uguale a 8n +6. Con l’integrazione (considerando n continuo…) ho pensato allora di fare 4n^2 + 6n ma ho visto che poi per rispettare i valori 9-23-45-… dovevo togliere il polinomio 4n-3 e quindi
4n^2 +6n -4n +3 = 4n^2 +2n +3.
La funzione mi fa ottenere correttamente i valori dei rimbalzi per n da 1 a 4 e quindi all’ottavo tentativo mi vengono 275 rimbalzi e 423 rimbalzi per il decimo tentativo (risolvendo l’equazione di 2o grado).
Immagino che l integrale non funzionasse bene perché f(n+1)-f(n) non e una vera e propria derivata ma non so se questo sia giusto.
Ottimo, anche a me viene così. A dopo per la soluzione argomentata.
1 quesito…45 cm cioè 15 sun
2 quesito…275 rimbalzi e 10 tentativi
Bene, se vuoi proporre anche il procedimento, così poi ci confrontiamo. Grazie.
1 quesito…ho trasformato i sun in centimetri …ho sottratto dal totale i 2 lati più lunghi …ho diviso per 3 e ho ottenuto 45 cm cioè che 15 sun..
2 quesito..ho calcolato la regolarità nella successione..cioè +8 e poi ho calcolato fino ad arrivare alle 2 conclusioni richieste.
Bene, a domani pomeriggio per le soluzioni argomentate,
1 quesito…45 cm cioè 15 sub
2 quesito…275 rimbalzi e 10 tentativi
1) (87 – 2 x 21)/3 = 15
Bene. A domani pomeriggio per le soluzioni argomentate.
Sono d’accordo con Andrea Cravero, ho ottenuto gli stessi risultati per i 2 problemi, propongo per il secondo la successione definita per ricorrenza:
primo elemento = 9
elemento enne-esimo = elemento (enne – esimo-1) +14+8(n-2)
Grazie di questa sollecitazione che mi ha spinto a cercare info su questa arte antica e suggestiva. Il wasan era praticato da studenti ma anche da persone comuni, che affrontavano problemi matematici per divertimento e per risolvere le necessità della vita quotidiana, come costruire un ventaglio e disporre i fiori nei vasi. I quesiti erano disegnati su piccole tavolette di legno, i sangaku, che venivano appese di fronte ai templi per sfidare i passanti a scrivere la soluzione sul retro della tavola.
Felice di aver stimolato questa ricerca, oltre la matematica, tra arte e vita quotidiana.
Anche se mi viene da sorridere pensando che tra le necessità ci sia quella di costruire un ventaglio!! Altri tempi!!
1) Se C è il lato corto e L quello lungo, si ha 3C+2L=87 sun. Sostituendo L=21 sun si ottiene 3C=45 sun e quindi C=15 sun.
2) Ad ogni tentativo il numero di rimbalzi aumenta di 8 in più rispetto al tentativo precedente (14, 22, 30…). Quindi il numero di rimbalzi al tentativo N è dato da 9+sommatoria(6+8N) con N=1,2,3…La serie è quindi 9, 23, 45, 75, 113, 159, 213, 275, 345, 423…Ci vogliono dieci tentativi (N=10) per arrivare a 423 rimbalzi. Dopo 8 tentativi si è a 275 etc.
Bene, a domani per le soluzioni argomentate.