
I Giochi del Lunedì di Prisma del 21 aprile 2025 a cura di Fabio Ciuffoli
Oggi presentiamo 4 problemi tratti dall’interessante rubrica “La vita matematica” pubblicata su HuffPost Italia. La rubrica settimanale, curata da Franco Torre ingegnere e appassionato di matematica, propone stimolanti problemi di geometria, di logica e considerazioni generali sulla storia della ‘regina delle scienze’. Invitiamo i lettori a inviarci osservazioni, proposte di soluzione e problemi simili utilizzando lo spazio dei commenti. Domani alle ore 17.00 pubblicheremo le soluzioni.
La vita matematica
1. Il Serbatoio. Un serbatoio pieno d’acqua perde ogni giorno un decimo del suo contenuto. Dopo quanto tempo si sarà svuotato della metà?
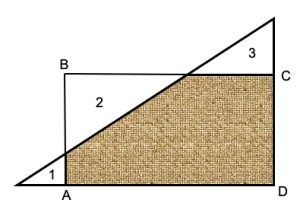
2. Quattro triangoli. Quattro triangoli rettangoli e un rettangolo sono disegnati in figura. Le aree 1, 2 e 3 valgono, rispettivamente, 5, 45 e 20. Quanto vale l’area colorata del rettangolo ABCD?
3. Il problema delle due candele.

Due candele a forma di cilindro, di differente diametro ma della stessa altezza come schematizzato in figura, vengono accese contemporaneamente. Entrambe bruciano a velocità costante, la a brucia completamente in 10 ore, la b in 8 ore. Dopo quanto tempo dall’accensione l’altezza della candela b sarà la metà dell’altezza dell’altra candela?
4. Tre coppie di fidanzati. Marcello e Claudia, Giuseppe e Roberta, Luca e Michela sono tre coppie e delle loro età si sa che:
Che età hanno i tre ragazzi?
I problemi sono tratti dalla rubrica settimanale ”La vita matematica” pubblicata su Huff Post Italia a cura dell’ing. Franco Torre.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
12 risposte
147.2
Let x, y be the legs of the larger triangle. The area sought will be
R=xy/2-5-20=xy/2-25
The triangles are all similar. Let’s call T the area of the large triangle i.e. T=xy/2 so
(1) R=T-25.
Let r=x/y then the area T of the large triangle is
(2) T=½ry²,
meaning what
(3) y=√(2/r)√T
Let A, B, C be the areas 1, 2, and 3 and a, b, and c be the legs corresponding to y in the similarity.We can write
y=a+b+c
using (3) written for y, for a, b and c:
y=√(2/r)(√A+√B+√C)
so y²=2/r5(1+3+2)² and by (2)
T=5(6)² and by (1):
R=180-25=155.
147.1
Sia n il numero di giorni.
(9/10)ⁿ=1/2
n=log2/(log10-log9)≈6g 13h 53′ 29″.
147.3
h-h/8t=½(h-h/10t)
2-1/4t=1-1/10t
t=20/3 6h40′.
Perfetto, a domani pomeriggio per tt le soluzioni commentate.
1. log in base 0.9 di 0.5 = ~6.5788 giorni
2. 155
3. Altezza delle candele unitaria. Grafico spazio tempo, x è il tempo dopo il quale a sarà il doppio di b. Due similitudini:
(8-x):y = 8:1
(10-x):(2y) = 10:1
y = 1/6 (altezza di b nell’istante x), altezza di a = 1/3
x = 20/3 = 6h:40′
4. Marcello 23, Giuseppe 26, Luca 27
Ottimo Giorgio, come sempre. La soluzione geometrica, che avevo in mente per il problema 3, è quella che hai presentato.
Dalla combinazione di 2 e 3 di ottiene subito che Giuseppe ha 26 anni e Roberta 21 anni.
Perciò, dalla combinazione della 1 e della 3 si ha che la somma delle età di Claudia e Michela è 40 anni.
Ma per la 4 Michela deve avere più di 21 anni perciò Claudia deve avere meno di 19 anni ed è quindi la più giovane. Cioè, sempre per la 4, Michela ha 22 anni e Claudia ha 18 anni.
Allora, per la 3, Luca ha 27 anni e Marcello ha 23 anni.
In definitiva:
Marcello ha 23 anni e Claudia ha 18 anni
Giuseppe ha 26 anni e Roberta ha 21 anni
Luca ha 27 anni e Michela ha 22 anni
6 ore 40 min
Ottimo, domani pomeriggio le soluzioni commentate
problema 4
luca 27
marcello 23
giuseppe 26
Ottimo a domani per tt le soluzioni commentate.
I 4 triangoli
2*A1 = x*y; 2*A2:2*A1 = h^2:1 => h^2 = 9 e h = 3, analogamente 2*A3:2*A1 = k^2:1 => k^2 = 4 e k = 2; altezza rettangolo x + hx = 4x, base rettangolo hy + ky = 5y, area rettangolo 4x * 5y = 200. Area richiesta 200 – 45 = 155.
Problema 2 – Quattro triangoli
xy = 10
k^2 xy = 90 => k = 3
q^2 xy = 40 => q = 2
Area rettangolo=(x+kx)(ky+qy) = xy(k+1)(k+q) =10 × 4 × 5 = 200.
3. Problema delle candele.
ha = (H – Ht) / 10
hb = (H – Ht) / 8
hb = ha / 2. => (H – Ht) / 8 = [(H – Ht / 10)] / 2
2 – t/4 = 1 – t /10.
1 = t/4 – t/10.
20 = 5t – 2t
3t = 20
t = 20/3 di ore ossia 6 ore 40 min.
(400 minuti)