145. Soluzioni del 24 marzo 2025 – Colloquio per PayPal

Soluzioni del 24 marzo 2025 a cura di Fabio Ciuffoli 

Ieri abbiamo presentato 4 problemi utilizzati come punto di partenza per i colloqui di lavoro a Paypal, la società di pagamenti on line fondata e gestita da Elon Musk, Peter Thiel e David Sacks, a Palo Alto nel 2000. Raccogliamo con piacere lo stimolo fornito da Fabio DF che ha proposto un’interessante variante del problema 4. I lampioni. Di seguito pubblichiamo le nostre proposte di soluzione. 

Colloquio per Paypal – soluzioni 

1. Due corde. Ci sono due corde, ogni corda ha una densità variabile nella sua lunghezza in modo che brucia a una velocità diversa dall’altra, ma ciascuna impiega un’ora per bruciare completamente. Come utilizzeresti le due corde per misurare 45 minuti? 

1. Soluzione: Accendi contemporaneamente entrambe le estremità di una corda e un’estremità dell’altra corda. Le estremità in fiamme della prima corda si incontreranno dopo mezz’ora. In questo momento ci sarà ancora mezz’ora di fuoco sulla seconda corda, quindi accendi la sua seconda estremità e quando i due capi bruciati della seconda corda si incontreranno saranno trascorsi altri 15 minuti. In questo modo il tempo totale trascorso dalla prima accensione è di 45 minuti.

2. Dividi e conquista. I numeri interi possono avere un numero dispari di divisori o un numero pari. Ad esempio i divisori di 4 sono 1, 2 e 4, per cui 4 ha tre divisori, quindi un numero dispari di divisori; i divisori di 24 sono 1, 2, 3, 4, 6, 8, 12 e 24, sono otto divisorii e perciò 24 ha un numero pari di divisori. Quali numeri interi hanno un numero dispari di divisori?

2. Soluzione: I numeri interi che hanno un numero di divisori dispari sono i numeri quadrati: 1, 4, 9, 16, 25, 36…. In generale, sia Z un numero intero e D un divisore di Z. Se D è un divisore, allora esiste un altro divisore, che indichiamo con D*, tale che D • D* = Z. Nell’esempio di Z = 24, se D = 2, l’altro divisore è D* = 12. Possiamo accoppiare ogni divisore D con il suo complemento D*. Tutti i numeri interi hanno quindi un numero pari di divisori, a meno che il numero non sia quadrato, poiché in questo caso esiste un divisore D = D*. La domanda richiede divisori ‘univoci’ quindi se D = D*, contiamo D solo una volta come divisore, perciò il numero totale di divisori di un numero quadrato è un numero pari + 1, cioè un numero dispari.

3. Enigma delle monete. C’è un tavolo circolare di diametro non specificato. Tu e il tuo avversario avete una notevole scorta di monete di dimensioni identiche. Il gioco prevede che ognuno a turno, metta una moneta sul tavolo. Nessuna moneta può essere spostata dopo il posizionamento e nessuna moneta può essere posizionata interamente o parzialmente sopra un’altra. Il primo giocatore che non riesce a piazzare una moneta perde. Puoi scegliere se iniziare per primo o per secondo. Qual è la tua strategia per assicurarti la vittoria?

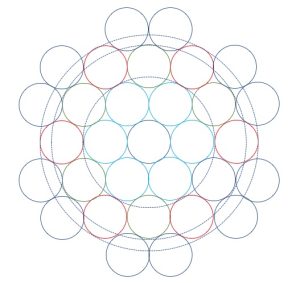
3. Soluzione: Inizia per primo e metti la tua moneta al centro del tavolo. Quando il tuo avversario mette una moneta sul tavolo, tu la metti nella posizione esattamente opposta, cioè a 180 gradi rispetto al centro del tavolo. Ci sarà sempre un posto in quella posizione e alla fine, il tuo avversario rimarrà senza spazio, qualsiasi siano le dimensioni del tavolo. In fotografia a sinistra è illustrata la disposizione delle prime sette monete. Nel disegno a destra è riportato uno schema nel quale si mostra che a partire dal centro le monete aggiunte, sulla stessa circonferenza, sono sempre di numero pari per cui a occupare lo spazio di una nuova circonferenza e perciò non trovare posto sul tavolo sarà sempre il secondo giocatore.

4. I lampioni. In una strada ci sono 100 lampioni, ciascuno regolato da un suo interruttore. Sono tutti spenti, quando passa di lì un bambino che schiaccia tutti gli interruttori e così li accende tutti. Dopo di lui passa un secondo bambino che schiaccia gli interruttori della tabellina del 2 e spegne tutti quelli che tocca. Un terzo bambino schiaccia gli interruttori della tabellina del 3 e in questo modo spegne alcuni lampioni e ne accende altri. Un quarto bambino cambia di segno agli interruttori della tabellina del quattro e così via fino all’ultimo bambino. Dopo che è passato il centesimo bambino, quali lampioni saranno accesi? E c’è una regola in generale?

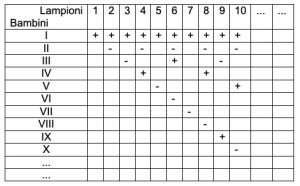
4. SOLUZIONI. Il problema dei lampioni presenta molte analogie con il problema 2 Dividi e conquista. In tabella riportiamo uno schema semplificato riferito a 10 lampioni (in riga) e 10 bambini (in colonna) con i segni + e – per indicare rispettivamente acceso e spento. Il primo bambino accende tutti i lampioni quindi avranno tutti segno positivo. Il secondo bambino cambia di segno ai lampioni 2, 4, 6, 8, 10 che ora avranno segno negativo. Il terzo bambino cambia segno ai lampioni 3, 6, 9. Il quarto bambino accende il lampione 4 e spegne il lampione 8 e così procedono anche gli altri bambini. Rileviamo, a conferma della spiegazione fornita al problema 2, che restano accesi i lampioni 1, 4 e 9 che sono esattamente i numeri quadrati. 

Più in generale, un lampione resta acceso se il numero dei  suoi divisori è dispari. I divisori di un intero vanno a coppie. Indicando con L i lampioni e con N i bambini, se L è divisibile per N allora L è anche divisibile per L/N a sua volta intero, quindi per ogni accensione ci sarà un corrispondente spegnimento, poiché i divisori sono in numero pari. L’unica eccezione è quando N è radice quadrata di L, in questo caso infatti L/N coincide con N, i divisori di L sono in numero dispari e il lampione si troverà in posizione acceso. In conclusione rimangono accesi i lampioni 1, 4, 9, 16, 25, 36, 49, 64, 81, 100  per un totale di dieci lampioni.

A seguito dell’interessante confronto con Fabio DF riportiamo il problema che ha proposto e la nostra soluzione.

Tutti i lampioni, tranne il primo, sono spenti. Ci sono 999 (da 2 a 1000) bambini ognuno dei quali gioca con i lampioni nel seguente modo:

– il bambino 2 preme l’interruttore sul lampione 2 e, di conseguenza, cambia lo stato del lampione 2 e di tutti i suoi multipli;

– il bambino 3 preme l’interruttore sul lampione 3 e, di conseguenza, cambia lo stato del lampione 3 e di tutti i suoi multipli;

– e così via fino al 999 esimo bambino.

Ora, se volessimo accendere tutti i lampioni, quali bambini sarebbe necessario far giocare?

P.S. ovviamente, il bambino 1 non può far parte del gioco altrimenti sarebbe stato banale

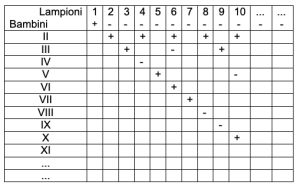
SOLUZIONE. In tabella riportiamo lo schema empirico riferito ai primi 10 bambini e 10 lampioni. Per accendere tutti i lampioni il bambino contrassegnato con IV non dovrà giocare altrimenti il lampione 4 resterebbe spento. Allo stesso modo anche i bambini VIII e IX non dovranno giocare. Procedendo con lo schema si rileva che non dovranno giocare i bambini XII, XVI, XVIII, XX, XXIV, XXV, XXVII, XXVIII, XXXII, XXXVI ecc.

In generale non dovranno partecipare i bambini contrassegnati con un numero quadrato (4, 9, 16, 25, 36, 49 ecc.) e i bambini contrassegnati con un multiplo di un numero quadrato (8, 12, 16, 20, 24 … e 18, 27, 36, 45 … e 25, 50, 75, 100 … ecc.). In altri termini, per accendere tutti i lampioni devono partecipare i bambini contrassegnati da numeri “piatti” ossia quei numeri in cui nella scomposizione in fattori primi ogni fattore appare al più con potenza di 1.     

Per chiarezza e miglior comprensione, alleghiamo una tavola delle scomposizioni in prodotto di fattori primi dei numeri da 1 a 100. I bambini con i numeri che nella colonna scomposizione non riportano esponenti dovranno partecipare. Ovviamente come già precisato va escluso il bambino 1.

I Giochi del Lunedì di Prisma tornano tra due settimane.