141. Soluzioni del 27 gennaio 2025 – Una stella nel cerchio e un mazzo di carte

Soluzioni del 27 gennaio 2025 a cura di Fabio Ciuffoli 

Ieri abbiamo presentato due problemi proposti nell’ambito di uno stage di matematica per allievi liceali. Due bellissimi problemi, con un ottimo mix teorico e empirico. Di seguito pubblichiamo le nostre proposte di soluzione. 

Una stella nel cerchio e un mazzo di carte – soluzioni 

1. La stella nel cerchio. In una bandiera rettangolare è disegnata una stella a cinque punte regolare, inscritta in un cerchio di raggio 7 cm, come in figura.

A. Calcolare l’area della stella.

B. Se una mosca puntiforme vola contro la bandiera, qual è la probabilità che finisca nella zona colorata in verde? I lati del rettangolo sono in rapporto 2:3.

1. SOLUZIONE. A. L’area della stella è composta da cinque deltoidi (o aquiloni) a sua volta composti da due triangoli uguali con un lato in comune che misura 7 cm e con angoli 18°, 126° e 36°, come evidenziato in figura.

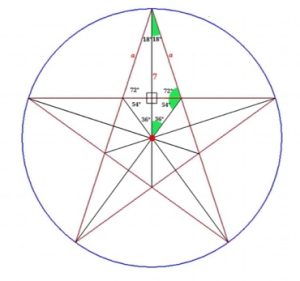
Con il teorema dei seni calcoliamo il lato a = 7sen36°/sen126° = 5,0858 cm. Ora calcoliamo l’altezza del triangolo, relativa alla base a, e avremo h = 5,0858sen18°/sen90° = 1,5716 cm. Infine area della stella = 10(7 • 1,5716)/2  = 55,006 cm².

Un altro modo per determinare l’area della stella, proposto da Carmelo Giugno e illustrato in figura, prevede il calcolo dell’area gialla e la successiva moltiplicazione per 5.

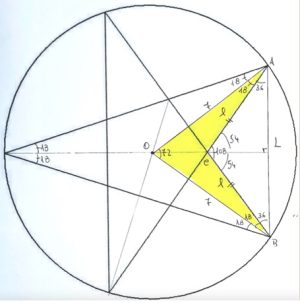
Area stella = 5(Area_(AOB) – Area_(ACB)]

Indicando con AB = L e AC = BC = l  si avrà: L = 2 • 7sen36° = 14sen36°

l = L/2sen54° = 7sen36°/sen54° e infine area stella = 5[(7²/2)sen72° – (7²/2) (sen36°/sen54°)²sen108°] = 55,006 cm².

Per chi volesse risparmiarsi un po’ di calcoli …conoscendo il raggio della circonferenza circoscritta r, l’area della stella è pari a:

Ulteriore considerazione, il rapporto tra l’area del cerchio e l’area della stella è costante:  Area(cerchio)/area(stella) = costante.

B. La probabilità che una mosca puntiforme finisca nella zona colorata in verde è data dal rapporto tra area verde e area totale.

Area verde = Area cerchio – Area stella = π72 – 55,006 = 98,854 cm2.

Area bandiera = 14 • 21 = 294 cm2.

Probabilità = 98,854/294 = 0,3362 quindi 33,62%

2. Il mazzo di carte. In un mazzo di 2023 carte con il dorso in su, si prendono 100 carte in cima al mazzo, si capovolgono una a una e si mettono in fondo al mazzo. Ora si ha un mazzo in cui non tutte le carte sono con il dorso in su: le ultime 100 sono girate al contrario. Si ripete la stessa operazione fino a quando non si ottiene nuovamente un mazzo con tutte le carte con il dorso in su. Quanti mazzetti di 100 carte saranno stati capovolti in totale?

2. SOLUZIONE. Iniziamo illustrando il procedimento empirico. Per semplificare prendiamo un mazzo da 3 carte totali dal quale capovolgiamo mazzetti da 2 carte alla volta. In tabella riportiamo i risultati.

Rileviamo con facilità che dopo tre capovolgimenti le carte tornano allo stato iniziale e ciascuna carta viene capovolta due volte. Indichiamo con x il numero dei mazzetti da girare e con y il numero di volte che ogni carta verrà girata, che dovrà essere pari altrimenti sarebbe girata in su, avremo 2x = 3y in cui x e y devono essere interi e inoltre y deve essere pari. Ora andiamo a sostituire y con i numeri pari, a partire dal minimo 2, allora x è 3, quindi occorrono tre capovolgimenti.

Secondo esempio con un mazzo da 10 carte totali, capovolgiamo 4 carte alla volta.

Con 5 capovolgimenti le carte tornano allo stato iniziale e ogni carta viene capovolta due volte. In formule 4x = 10y (dove x e y numeri interi positivi e y pari) e andando a sostituire y con un numeri pari a partire da 2 avremo 4x = 20 da cui x = 5.

Terzo esempio con un normale mazzo di 52 carte e capovolgendo mazzetti da 10 carte alla volta.

Passaggi conteggiando le carte rivolte in su: 42 32 22 12 2; 8 18 28 38 48; 46 36 26 16 6; 4 14 24 34 44; 50 40 30 20 10 0.

Ora sono tutte capovolte, quindi medesimo numero di passaggi per chiudere la rotazione: 10 20 30 40 50;  44 34 24 14 4; 6 16 26 36 46; 48 38 28 18 8; 2 12 22 32 42 52. Quindi 52 passaggi complessivi.

In formule 10x = 52y (con x e y interi positivi e inoltre y deve essere pari). In questo caso avremo 10x = 52y semplificando 5x = 26y. Andando a sostituire y con i numeri pari a partire dal minimo 2, troveremo che y deve essere 10 così x = 52, quindi 52 capovolgimenti totali con ogni carta che viene capovolta 10 volte

Infine risolviamo il problema nel testo. Indicando con x il numero dei mazzetti da girare e con y il numero di volte che ogni carta verrà girata, affinché tutte le carte tornino alla situazione iniziale avremo:

100x = 2023y (con x e y interi positivi e y pari)

Scomponendo: 100 = 22 * 52;  2023 = 7 * 172. I numeri 100 e 2023 sono coprimi, non hanno divisori comuni. Quindi avremo: y minimo = 100;  x minimo = 2023

Quindi dovranno essere girati 2023 mazzetti da 100 carte ciascuno e ogni carta verrà capovolta 100 volte.

I Giochi del Lunedì tornano tra due settimane.