
I Giochi del Lunedì di Prisma del 13 gennaio 2025 a cura di Fabio Ciuffoli
I quattro problemi che proponiamo oggi provengono da una recente prova di matematica (Dürer Math Competition) per ragazzi ungheresi di età tra i 14 e i 16 anni. L’Ungheria ha acquisito una reputazione di eccellenza in matematica a metà del secolo scorso, grazie a grandi scienziati come John von Neumann, Edward Teller, Eugene Wigner, Paul Erdos, George Polya, Paul Hzalmos e altri ancora. Divennero famosi come ‘Marziani’ per la provenienza da una piccola nazione e per la stana lingua parlata e anche perché scherzavano dicendo che un’intelligenza aliena superiore era già sbarcata sulla (loro) Terra. In ogni caso, l’Ungheria è sempre stata all’avanguardia nella divulgazione scientifica. Infatti è stato il primo paese al mondo ad avviare una competizione di matematica per adolescenti nel lontano 1894 e, possiamo dire, la tradizione continua. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti. Domani pomeriggio alle ore 17.00 pubblicheremo le soluzioni commentate.
Matematica dall’Ungheria
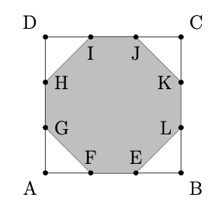
1. Piantare papaveri. Morfeo, il dio dei sogni, ha un giardino quadrato ABCD di lato 30 metri. Vuole piantare il papavero nell’ottagono definito dai punti di trisezione EFGHIJKL. Qual è l’area di questo ottagono in metri quadrati?
2. L’esercito di Ares. Ares è a capo di un esercito composto da Centauri, Uomini e Cavalli Alati. Ognuno ha 1 testa, i Centauri e i Cavalli Alati hanno 4 gambe, gli Uomini hanno 2 gambe, mentre i Centauri e gli Uomini hanno 2 braccia, mentre i Cavalli Alati non hanno braccia. Sapendo che ci sono 193 teste, 666 gambe e 244 braccia, quanti Centauri fanno parte dell’esercito di Ares?
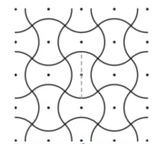
3. Tessere Testa d’Ascia. I bordi di queste tessere identiche sono quarti di cerchio e i loro centri sono i punti contrassegnati. Determinare l’area di una piastrella, misurata in cm2, sapendo che l’altezza di una piastrella, tratteggiata in figura, è 12 cm.
Aggiornamento per le soluzioni click qui.
I problemi sono tratti dalla Competizione di matematica Dürer, rivolta a ragazzi dai 10 ai 18 anni che si svolge in Ungheria dal 2007. È stata fondata da un gruppo di studenti del primo anno dell’università ELTE di Budapest, che volevano creare un concorso divertente, meno formale (e meno difficile) rispetto alle competizioni più tradizionali come le Olimpiadi di Matematica. Il concorso ha portato nuova energia alla divulgazione della matematica in Ungheria, e una selezione delle sue domande è appena stata pubblicata nel libro ‘Esplorazioni matematiche per giovani menti’ di Bàlint Hujter, Daniel Lenger e Gabor Szucs.
https://durerinfo.hu/durer-in-english/durer-in-english-take-part-in-the-competition/
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
14 risposte
Problema 4
Problema 1 – Basta togliere due quadrati di lato DH.
1) 700m²
2) 69C. 53U. 71C.A.
3) A(piastrella)=72cm²
4) A(grigia)=1296pi cm²
Ottimo, nel pomeriggio le soluzioni.
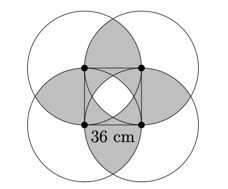
Risposta 4. Via geometrica L’area grigia è uguale all’area del cerchio, quindi 1296π cmq
L’area grigia è uguale all’area del cerchio, quindi 1296π cmq
Risposta 4.
L’area Grigia scomposta in 4 aree di colore Arancione, Verde e Rosa ha misura G=4A+4V+4R = πr^2 con r lato del quadrato: dimostrazione visuale in 4 passi.
Risposta 4. Via algebrica
B:=? ‘area Blu
R:=? ‘area Rosa unitaria
V:=? ‘area Verde unitaria
A:=2R+V+B=? ‘area Arancione unitaria
C:=? ‘area Celeste unitaria
M:=R+V=? ‘area Marrone unitaria
G:=4A+4V+4R = ? ‘area Grigia
Q:=B+4V+4R=V+2M+A=r^2 ‘area del quadrato di lato r o raggio del cerchio (noto)
3Q=6V+4M+2A+4R+B=(B+4V+4R)+(4M+2A+2V)
O:=C+M+2A+2V+3R+B=2C+2A=π*Q=π*r^2 ‘area dei cerchi di raggio r (noto)
M+A=O/4=π*r^2/4
Posti a sistema algebrico:
A=2R+V+B
B+4V+4R=Q
V+2M+A=Q
M=R+V
C+M+2A+2V+3R+B=π*Q
2C+2A=π*Q
4M+4A=π*Q
Risolvo con sostituzioni
B=A-2R-V, A-2R-V+4V+4R=Q
A+2R+3V=Q, 2R=Q-A-3V
4M+4A=π*Q, M=π*Q/4-A
2C+2A=π*Q, C=π*Q/2-A
V+2M+A=Q, V=Q-π*Q/2+2A-A=A+(2-π)*Q/2
R=M-V=π*Q/4-A-A-(2-π)*Q/2=(3π-4)*Q/4-2A
Soluzioni reali
B=4A-π*Q+Q
C=π*Q/2-A
M=π*Q/4-A
R=(3π-4)*Q/4-2A
V=A+(2-π)*Q/2
Infine G=?
G=4A+4V+4R=4A+4A+2*(2-π)*Q+(3π-4)*Q-8A=4Q-2πQ+3πQ-4Q=πQ
Soluzione problemi 2 e 3 vedi immagini allegate.
Soluzione problemi 2 e 3 vedi immagini allegate
Problema 3
I punti di intersezione tra i semicerchi determinano un quadrato di diagonale 12u. L’area della piastrella è pari all’area del quadrato, poiché ciò che esubera è pari a ciò che manca. Il quadrato è anche un rombo, la sua area è pari al prodotto delle diagonali diviso 2, quindi è 72
1. Quadrato di lato 30 cm meno 2 quadrati di lato 10 cm = 900-200 = 700 m^2.
2. 69 Centauri, 53 Uomini, 71 Cavalli Alati.
3. Quadrato di diagonale 12 cm. Area 72 cm^2.
4. Cerchio di raggio 36 cm = 1296PI cm^2.
Ops nel primo i lati sono in metri. 😉
Ottimo, Giorgio, come sempre. A presto 👋