Soluzioni del 16 dicembre 2024 a cura di Fabio Ciuffoli
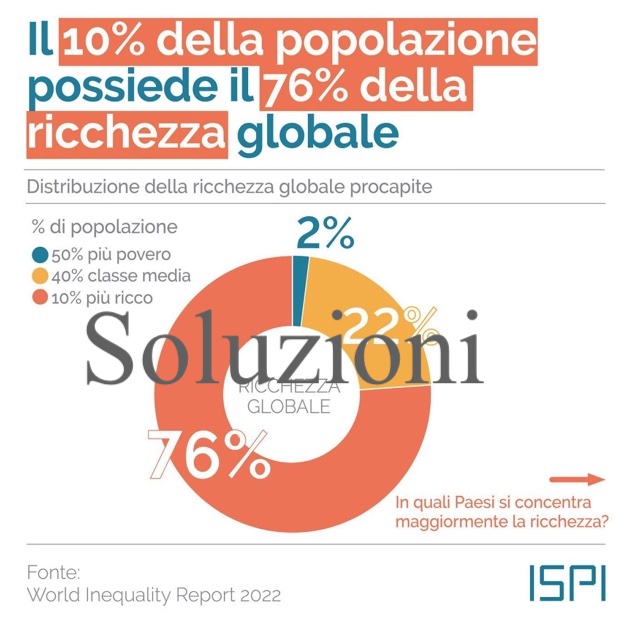
Ieri abbiamo proposto due problemi prendendo spunto dalla poesia ‘La Statistica’ di Trilussa relativi alla concentrazione dei consumi e della ricchezza. Di seguito presentiamo le nostre proposte di soluzione.
La Statistica e i polli di Trilussa – soluzioni
1. Esercitazione svolta. Cinque persone hanno mangiato cinque polli: Aldo ha mangiato un pollo e mezz0; Bruno zero polli; Carlo un pollo; Dario zero polli ed Enrico due polli e mezzo.
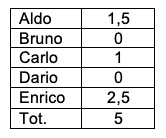
Determinare la media aritmetica, la mediana, la moda, la varianza, lo scarto semplice, lo scarto quadratico medio, l’indice Gini e la Curva di Lorenz.
1. SOLUZIONE esercitazione. Presentiamo di seguito la soluzione dell’esercitazione e successivamente due casi estremi : CASO A massima concentrazione (i cinque polli sono mangiati da una sola persona); CASO B massima uguaglianza (ogni persona mangia un pollo).
Media aritmetica: somma dei valori / n. totale dei valori = (1 + 0 + 1,5 + 0 + 2,5)/5 = 1
Mediana: si ordinano i valori dal più piccolo al più grande e si individua quello di mezzo: 0 + 0 + 1 + 1,5 + 2,5 mediana = 1.
Moda: valore che compare con maggior frequenza = 0
Campo di variazione: valore massimo – valore minimo = 2,5 – 0 = 2,5
Scarto semplice medio: media degli scarti presi in valore assoluto: (1 + 1 + 0 + 0,5 + 1,5)/5 = 0,8
Varianza: media degli scarti elevati al quadrato [(-1)2 + (-1)2 + 02 + 0,52 + 1,52)/5 = 0,9
Scarto quadratico medio: radice quadrata della varianza √ 0,9 = 0,95
L’indice Gini è un coefficiente che misura il livello di concentrazione di un fenomeno. Viene spesso utilizzato per verificare se variabili, come il reddito, la ricchezza o in questo caso il consumo di polli, siano più o meno equidistribuiti in una popolazione. C’è equidistribuzione se il fenomeno ha la più bassa concentrazione possibile, quando ciascun individuo possiede la stessa quantità della media dei dati, mentre c’è concentrazione massima se un solo individuo possiede tutta la quantità e gli altri nulla. L’indice Gini è sempre compreso tra 0 (caso di equidistribuzione) e 1 (caso di massima concentrazione). Per il calcolo dell’indice Gini e per la costruzione della Curva di Lorenz si predispone la seguente tabella.
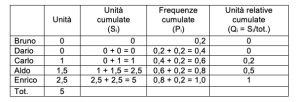
Le unità sono i polli consumati ordinati in modo crescente; le unità cumulate (Si) sono le somme graduali dei consumi accumulati; le frequenze cumulate (Pi) sono le quote di persone, che consumano una determinata unità, appunto accumulate; le unità relative cumulate (Qi = Si /tot.) sono le proporzioni di unità consumate dalle rispettive quote di persone Pi accumulate.
Ora possiamo utilizzare la formula dell’indice di Gini
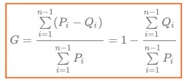
andando a sostituire G = 1- [(0,2 + 0,5) / (0,2 + 0,4 + 0,6 + 0,8)] = 1 – (0,7 / 2) = 0,65.
In generale è possibile interpretare il livello di concentrazione di Gini:
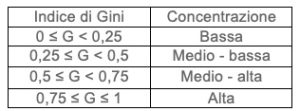
Nel nostro caso rileviamo una concentrazione medio-alta.
La Curva di Lorenz. Il livello di concentrazione si può rappresentare graficamente mediante la Curva di Lorenz ossia un grafico ottenuto unendo con segmenti i punti di coordinate Pi, Qi definiti in tabella, che formano una spezzata. La regione del grafico delimitata dalla Curva di Lorenz e dalla bisettrice indica la concentrazione del fenomeno: maggiore è tale area maggiore è la concentrazione.
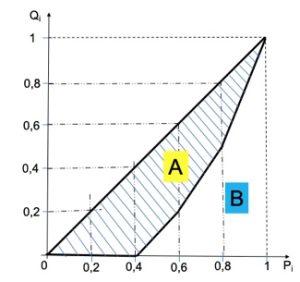
L’indice Gini e la Curva di Lorenz rivelano una notevole concentrazione nel consumo di polli. Ad esempio, il punto di coordinate P3, Q3 indica che al 60% delle persone spetta solo il 20% dei polli totali.
Teoricamente, l’indice Gini rappresenta il rapporto tra le aree A / (A + B).
In conclusione, se avessimo utilizzato l’indice Gini o la Curva di Lorenz saremmo stati in grado di capire chi ha mangiato i due polli della poesia di Trilussa!
Come anticipato, presentiamo di seguito i calcoli e le tabelle riferiti ai due casi estremi: CASO A massima concentrazione (i cinque polli sono mangiati da una sola persona); CASO B massima uguaglianza (ogni persona mangia un pollo).
Caso A massima concentrazione
Media aritmetica: somma dei valori / n. totale dei valori = (0 + 0 + 0 + 0 + 5)/5 = 1
Mediana: si ordinano i valori dal più piccolo al più grande e si individua quello di mezzo: 0 + 0 + 0 + 0 + 5 mediana = 0.
Moda: valore che compare con maggior frequenza = 0
Campo di variazione: valore massimo – valore minimo = 5 – 0 = 5
Scarto semplice medio: media degli scarti presi in valore assoluto: (1 + 1 + 1 + 1 + 4)/5 = 1,8
Varianza: media degli scarti elevati al quadrato [(-1)2 + (-1)2 + (-1)2 + (-1)2 + 42]/5 = 5
Scarto quadratico medio: radice quadrata della varianza √5 = 2,24
Caso B massima equità
Media aritmetica: somma dei valori / n. totale dei valori = (1 + 1 + 1 + 1 + 1)/5 = 1
Mediana: si ordinano i valori dal più piccolo al più grande e si individua quello di mezzo: 1 + 1 + 1 + 1 + 1 mediana = 1.
Moda: valore che compare con maggior frequenza = 1
Campo di variazione: valore massimo – valore minimo = 1 – 1 = 0
Scarto semplice medio: media degli scarti presi in valore assoluto: (0 + 0 + 0 + 0 + 0)/5 = 0
Varianza: media degli scarti elevati al quadrato 02 + 02 + 02 + 02 + 02]/5 = 0
Scarto quadratico medio: radice quadrata della varianza √0 = 0
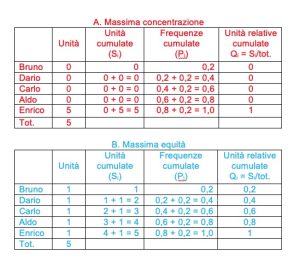
L’indice Gini
A. Massima concentrazione G = 1- [(0/(0,2 + 0,4 + 0,6 + 0,8)] = 1 – (0/2) = 1.
B.Massima equità G = 1- [(0,2 + 0,4 + 0,6 +0,8)/(0,2 + 0,4 + 0,6 +0,8)] 0 1 – (2/2) = 0.
La Curva di Lorenz
A. Massima concentrazione. L’area di concentrazione è massima, teoricamente data dall’area del triangolo rettangolo con ipotenusa la bisettrice del grafico e cateti 1.
B. Massima equità. L’area di concentrazione è nulla, quindi la spezzata coincide con la bisettrice nel grafico.
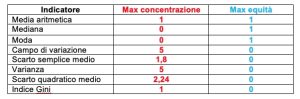
Riportiamo in tabella i vari indicatori a confronto tra massima concentrazione e massima equità.
La media aritmetica è uguale, come rileva Trilussa, ma tutti gli altri indicatori si collocano all’estremo opposto.
2. I redditi di sette famiglie. Sette famiglie percepiscono i seguenti redditi annui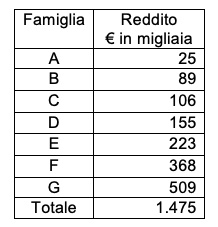
Determinare: la media, la mediana, il campo di variazione, lo scarto semplice medio, la varianza, lo scarto quadratico medio, l’indice Gini e la Curva di Lorenz.
2. SOLUZIONE.
Media aritmetica: (somma dei redditi / n. delle famiglie) 1.475.000/7 = € 210.71
Mediana: si ordinano i redditi dal minore al maggiore e si individua quello di mezzo € 155.000
Campo di variazione: (reddito massimo – reddito minimo) 509.000 – 25.000 = € 484.000
Scarto semplice medio: (media degli scarti presi in valore assoluto) = € 133.673
Varianza: (media degli scarti elevati al quadrato) = € 25.319.632.653
Scarto quadratico medio: (radice quadrata della varianza) = € 159.121
L’indice Gini è un coefficiente che misura il livello di concentrazione di un fenomeno. Viene spesso utilizzato per verificare se variabili, come il reddito o la ricchezza, siano più o meno equidistribuiti in una popolazione. C’è equidistribuzione quando il fenomeno ha la più bassa concentrazione possibile, questo accade se ciascun individuo possiede la stessa quantità della media dei dati, mentre c’è concentrazione massima quando un solo individuo possiede tutta la quantità e gli altri nulla. L’indice Gini è sempre compreso tra zero (caso di equidistribuzione) e uno (caso di massima concentrazione). Per il calcolo dell’indice Gini e per la costruzione della Curva di Lorenz è utile predisporre la seguente tabella.
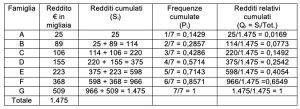
I redditi cumulati (Si) sono le somme dei redditi percepiti da ciascuna famiglia gradualmente accumulati; le frequenze cumulate (Pi) sono le quote di una famiglia sul totale delle famiglie gradualmente accumulate; i redditi relativi cumulati (Qi = Si /tot.) sono le proporzioni di reddito delle rispettive famiglie accumulate, sul totale dei redditi.
Applichiamo la formula dell’indice di Gini
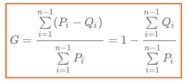
andando a sostituire G = 1- [(0,0169 + 0,0773 + 0,1492 + 0,2542 + 0,4054 + 0,6549) / (0,1429 + 0,2857 + 0,4286 + 0,5714 + 0,7143 + 0,8571)] = 1 – (1,558/ 3) = 0,4807.
La Curva di Lorenz. Il livello di concentrazione si può rappresentare graficamente mediante la Curva di Lorenz ossia un grafico ottenuto unendo i punti di coordinate Pi, Qi definiti in tabella sopra, con segmenti che formano una spezzata. La regione del grafico delimitata dalla Curva di Lorenz e dalla bisettrice indica la concentrazione del fenomeno: maggiore è tale area maggiore è la concentrazione.
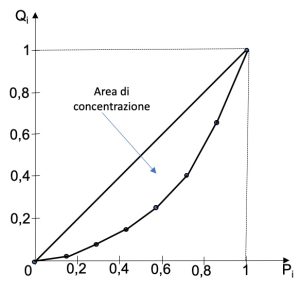
Tali valori indicano una notevole concentrazione, quindi la maggior parte del reddito totale è nelle mani di poche famiglie. Possiamo commentare il generico punto di coordinate (Pi, Qi), ad esempio (P3,Q3): il 42% circa delle famiglie più povere, percepisce quasi il 15% dei redditi totali.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).