
Soluzioni del 2 dicembre 2024 a cura di Fabio Ciuffoli
Ieri abbiamo presentato quattro problemi tratti dal nuovo libro ‘Matematica fuori dalle regole – Guida di sopravvivenza per genitori e insegnanti’ di Daniele Gouthier in libreria da circa un mese. Di seguito pubblichiamo le soluzioni commentate.
Matematica fuori dalle regole – soluzioni
1.1. Un paio di scarpe. Celeste va a comprare un paio di scarpe che costano 80 euro. Il cassiere, per errore, digita un prezzo aumentato del 20%. Per fortuna se ne accorge e, per rimediare, applica a Celeste uno sconto del 20%. In questo modo, Celeste paga il giusto?
1.2. Dopo che il cassiere ha erroneamente alzato il prezzo del 20%, di che percentuale dovrebbe abbassarlo per tornare al prezzo di partenza?
1.1. SOLUZIONE. Celeste non paga il giusto prezzo. Il 20% di 80 è 16 che sommato dà un prezzo erroneamente aumentato di 96 euro. Ora il 20% di 96 è 19,20 che sottratto a 96 dà un prezzo finale di 76,80 euro. Ovviamente i due risultati del 20% sono diversi in quanto applicati a importi che sono differenti. Il primo 20% è calcolato su 80 mentre il secondo 20% è calcolato su 96, la due quantità sono diverse e i risultati sono diversi.
1.2. SOLUZIONI. Per trovare questa percentuale immaginiamo di avere il prezzo aumentato 80 • 1,2 = 96. La domanda diventa per quale numero devo moltiplicare 96 per ottenere di nuovo 80 euro. Quindi 96 • x = 80 da cui x = 80/96 = 0,833 per cui la percentuale per tornare al prezzo di partenza è 1 – 0,833 = 0,167 quindi il 16,7%.
2. Le carte. Le carte in figura hanno un motivo da un lato e una vocale dall’altro. Celeste dice: “Se una carta ha lo sfondo a mattoncini, allora ha una ‘A’ dall’altro lato”. Per verificare se Celeste dice il vero, quali carte dobbiamo girare? Vogliamo girarne il meno possibile.

2. SOLUZIONE. Vanno girate tre carte: quella con lo sfondo a mattoncini, la ‘E’ e la ‘O’. Quella con lo sfondo a mattoncini perché dobbiamo verificare l’implicazione diretta: “Se il retro è a mattoncini, il fronte ha una A”. Le altre due perché dobbiamo verificare l’implicazione inversa: “Se il fronte non ha una A, il retro non è a mattoncini”. Sono le risposte a queste due domande che, assieme, ci dicono se Celeste dice il vero o meno.
3.1. Il torneo. A un torneo di tennis sono iscritti 128 giocatori. Il torneo è “a eliminazione diretta” ossia se due giocatori si incontrano, quello che perde esce dal torneo. Quante partite servono per determinare il vincitore?
3.2. E quante partite servono a determinare il vincitore di un torneo a eliminazione diretta al quale partecipano 256 giocatori? E se i partecipanti sono 100? E se sono 97? E se sono un numero generico n?
3.1. SOLUZIONE. Ci sono molti modi per risolvere questo problema, ad esempio con il calcolo diretto o il disegno dell’albero del torneo. Un modo semplice e intuitivo suggerisce di ragionare sulla domanda complementare: “Quante partite servono a eliminare i 127 giocatori che non vincono il torneo?”. In questa prospettiva il problema diventa facile: l’eliminazione diretta fa sì che ogni partita venga eliminato esattamente un giocatore. Quindi se dobbiamo eliminarne 127 per avere il vincitore, sono necessarie esattamente 127 partite.
3.2. SOLUZIONE. Se i partecipanti sono 256, servono 255 partite. Se sono 100, servono 99 partite. Se sono 97 partecipanti servono 96 partite e un giocatore sarà lievemente svantaggiato a causa del numero dispari di giocatori. In generale, indicando con n il numero dei giocatori, sono necessarie (n – 1) partite.
4. Il perimetro. Determinare il perimetro dell’edificio che ha la pianta disegnata in figura.
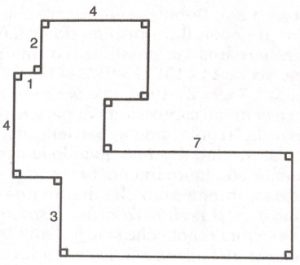
4. SOLUZIONE. I lati dell’edificio sono paralleli a due direzioni perpendicolari tra loro. I lati paralleli, disegnati in verticale, misurano (3 + 4 + 2) • 2 = 18. La misura dei lati paralleli disegnati orizzontalmente è un po’ meno immediata. Possiamo scriverla: 1 + 4 + x + 7 + y + z. É facile intuire quali lati sono indicati con x, y e z. Rileviamo inoltre che z + y = 1 + 4 + 7 – x da cui x + y + z = 1 + 4 + 7. Quindi la misura dei lati orizzontali è (1 + 4 + 7) • 2 = 24. Infine il perimetro è (18 + 24) = 42.
I problemi sono tratti dal libro “Matematica fuori dalle regole – Guida di sopravvivenza per genitori e insegnanti’ di Daniele Gouthier, Feltrinelli, Milano 2024.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).