136. Soluzioni del 18 novembre 2024 – Leonardo Pisano detto Fibonacci

Soluzioni del 18 novembre 2024 a cura di Fabio Ciuffoli

Ieri, per omaggiare il Fibonacci Day che cade il prossimo 23 novembre,  abbiamo presentato quattro problemi trattati da Leonardo Fibonacci protagonista, con sul suo Liberi abbaci, della grande rivoluzione economica, sociale e politica resa possibile da questa nuova matematica. Di seguito pubblichiamo le nostre proposte di soluzione. 

Leonardo Pisano detto Fibonacci

1. Un viaggiatore tocca successivamente Lucca, Firenze e Pisa, raddoppiando in ogni città il denaro con cui arriva e spendendo ogni volta 12 denari, per restare alla fine senza un soldo. Si chiede con quanto era partito.

1. SOLUZIONE. Impostiamo il problema con l’aiuto dell’algebra. Se chiamiamo x l’importo in denari con la quale il viaggiatore era partito, lasciando Lucca si ritroverà con 2x – 12 denari, che dopo la sosta a Firenze diventeranno 2(2x – 12) – 12= 4x – 36, e infine a Pisa saranno 2(4x – 36) – 12 = 8x – 84. Quest’ultima quantità va posta uguale a zero, 8x – 84 = 0 per cui x = 84/8 = 10,5 denari iniziali.

Per risolvere lo stesso problema, col metodo della doppia falsa posizione, si può supporre che fosse partito con 12 denari, nel qual caso a ogni tappa, e dunque anche alla fine, gli resterebbero 12 denari. Se invece fosse partito con 11 denari, rimarrebbe a Lucca con 22 – 12 = 10, a Firenze con 20 – 12 = 8 e infine a Pisa con 16 – 12 = 4 denari. Una diminuzione di un denaro all’inizio (da 12 a 11) ha portato a una diminuzione di 8 (da 12 a 4) nel risultato finale. Si dirà allora: per 1 che ho diminuito del capitale, mi sono avvicinato di 8; quanto dovrò ancora diminuire per avvicinarmi di altri 4?  Si moltiplica 4 per 1, e si divide per 8; verrà  ½ denaro, che tolto da 11 denari darà per il capitale iniziale 10 denari e ½.

2. Quattro uomini hanno acquistato un maiale per 60 soldi. Il primo volle avere un terzo di quel maiale, il secondo un quarto, il terzo un quinto, il quarto un sesto. Perciò pagando il primo 20 soldi per la terza parte del maiale, e il secondo, per la quarta parte, 15 soldi, e il terzo, per la quinta parte, 12 soldi, e il quarto per la sesta parte 10 soldi, e tutte queste somme insieme ammontano soltanto a 57 soldi. Si meravigliano che rimangano da pagare 3 soldi e chiedono chi di loro debba pagare.

2. SOLUZIONE. I 3 soldi mancano perché la somma delle parti non fa 1. Infatti 1/3 + 1/4 + 1/5 + 1/6 = 57/60 quindi mancano 3 soldi dei 60 totali.  Questi 3 soldi devono essere pagati in proporzione alle diverse quote di ciascun uomo, per cui si calcola il riparto:

[3/(20 + 15 + 12 + 10)] = 3/57 = 1/19 = 0,05263158 (coefficiente di riparto)

• (1/19)•20 = 20/19 al primo, che quindi dovrà pagare 21 + 1/19 soldi
• (1/19)•15 = 15/19 al secondo, che quindi dovrà pagare  15 + 15/19 soldi
• (1/19)•12 = 12/19 al terzo, che quindi dovrà pagare 12 + 12/19 soldi
• (1/19)•10 = 10/19 al quarto, che quindi dovrà pagare 10 + 10/19 soldi

3. Due uomini hanno denari e il primo dice all’altro: “Se mi dessi 7 dei tuoi denari, avrei 5 volte quello che ti resta”. L’altro risponde: “E se tu mi dessi 5 dei tuoi denari, avrei 7 volte quello che resta a te”. Si chiede quanto aveva ciascuno di essi.

3. SOLUZIONE. Indicando con x l’importo di denari del primo uomo e con y l’importo del secondo uomo, impostiamo il sistema con due equazioni e due incognite

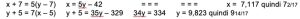
4. Un uomo compra 30 uccelli – pernici, colombi e passeri – per 30 denari, pagando 3 denari per una pernice, 2 denari per un colombo e un denaro per 2 passeri (ossia ½ denaro per passero). Vogliamo sapere quanti uccelli di ciascuna specie ha comprato.

4. SOLUZIONE. Indicando con x il numero delle pernici, con y quello dei colombi e con z quello dei passeri, possiamo formulare due equazioni:

• (1) x + y + z = 30 uccelli
• (2) 3x + 2y + 1/2z = 30 denari

Abbiamo due equazioni, tre incognite e sappiamo che i valori delle tre incognite devono essere numeri interi positivi. Raddoppiamo ogni termine nella seconda equazione così da renderli interi:

• (2) 6x + 4y + z = 60

Sottraiamo la prima equazione dalla seconda in modo da eliminare z, quindi  5x + 3y = 30

Dato che il primo e il terzo termine sono divisibili per 5, anche y sarà divisibile per 5; pertanto, y sarà uguale a 5 o a 10 o a 15 e così via. Ma y non può essere uguale a 10 o a un numero più grande, perché non sarebbe soddisfatta la seconda equazione, quindi y = 5. Ne segue che x = 3 e z = 22. Da notare che Leonardo risolve il problema con la stessa strategia usando però, come era solito, le parole e non i simboli matematici che utilizziamo oggi.

I Giochi del Lunedì tornano tra due settimane.