
Soluzioni del 4 novembre 2024 a cura di Fabio Ciuffoli
Ieri abbiamo presentato tre problemi, apparentemente complicati, che si possono risolvere con un’intuizione sorprendentemente semplice mediante l’utilizzo di una regola o di una comoda formula. Di seguito pubblichiamo le nostre proposte di soluzione.
Una tubazione e due cisterne -soluzioni
1. Un idraulico deve portare acqua attraverso un tubo dal punto A a un generico punto C che sei trova sul bordo di un deserto e poi dal punto C al punto B, come schematizzato in figura. Vengono date le dimensioni tra A e B e la distanza tra A e il confine del deserto. Dove dovrebbe essere posizionato il punto C, al bordo del deserto, in modo che la misura del tubo sia la più corta possibile?
Ci sono molti problemi di questo tipo che possono essere risolti senza usare il calcolo infinitesimale. Infatti, con una piccola intuizione si può “vedere” la soluzione.
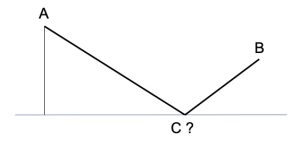
1. SOLUZIONE. Si determina il punto A’, speculare al punto A rispetto alla linea di confine del deserto, poi tracciando un segmento che collega il punto A’ con B, si individua il punto C, che indica la distanza più breve tra A’ e B, come illustrato in figura. Pertanto, quella posizione del punto C sul bordo del deserto permette la tubazione più breve.
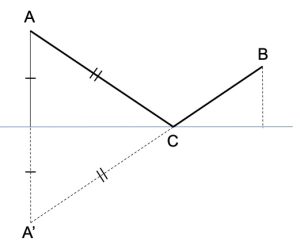
2. SOLUZIONE. Sorprendentemente, per trovare la dimensione x dei lati dei quadrati è sufficiente dividere la lunghezza del quadrato del foglio di zinco per 6. Nel nostro caso x = 120/6 = 20 cm. Di conseguenza, la cisterna avrà un volume di 80 per 80 per 20 = 128.000 cm cubi. E questo è il volume massimo che può essere raggiunto. Due prove empiriche non esaustiva ma significative: se la dimensione x del lato del quadrato fosse di 19 cm, il volume della cisterna sarebbe di 127.756 cm cubi; se la dimensione fosse di 21 cm, il volume della cisterna sarebbe di 127.764 cm cubi.
Una seconda semplice formula, per determinare direttamente il volume massimo della cisterna che si può ottenere da un foglio quadrato, indicando con a la misura del lato del foglio di zinco è 2a3/27 , nel nostro caso 2 • 1203/27 = 128.000 cm cubi.
Le due formule appena viste si applicano a lamiere quadrate. Si rinvia al prossimo problema per il caso della lamiera rettangolare e lo sviluppo del calcolo infinitesimale e della dimostrazione teorica.
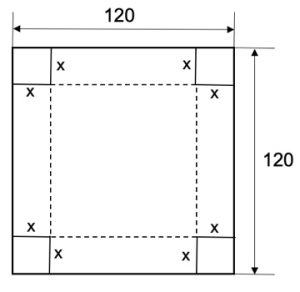
3. In questo caso l’idraulico dispone di un foglio di zinco rettangolare che misura 96 cm per 36 cm, come disegnato in figura. Ancora una volta, si desidera tagliare i quattro quadrati uguali agli angoli del foglio per ottenere una cisterna con il coperchio aperto. Quanto deve misurare il lato x dei quattro quadrati agli angoli se si vuole realizzare una cisterna a cielo aperto che contenga il massimo volume?
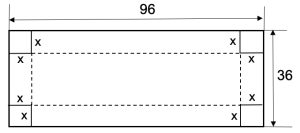
3. SOLUZIONE. Questo problema fu esposto nel libro Amusements in mathematics del genio inglese Henry Ernest Dudeney nel 1917. Per la soluzione, Dudeney propone una formula di nuovo sorprendentemente semplice, che può essere utilizzata per risolvere tutti gli enigmi di questo tipo, di cui il problema 2 è un caso particolare. Indicando con a e b i lati della lamiera e con x il lato dei quadrati da tagliare ai quattro angoli, la formula è x = [a + b – √(a2 + b2 – ab)]/6
Nel nostro caso x = [36 + 96 – √(1.296 + 9.216 – 3.456)]/6 = (132 – 84) / 6 = 8 cm.
Pertanto, le dimensioni della cisterna sono (96 – 16) cm per (36 – 16) cm per 8 cm, con un volume pari a 12.800 cm cubi. Anche in questo caso facciamo una prova empirica: se le dimensioni dei lati dei quadrati d’angolo fossero 7 cm, la cisterna avrebbe un volume massimo di 82 per 22 per 7 = 12.628 cm cubi; se invece le dimensioni dei quadrati d’angolo da ritagliare fossero 9 cm, la cisterna risultante sarebbe 78 per 18 per 9 = 12.636 cm cubi. Il problema che Dudeney ha posto e risolto utilizzando una semplice formula, viene affrontato teoricamente mediante il calcolo infinitesimale. Indicando con x il lato di ciascuno dei quattro quadrati d’angolo, il volume della cisterna può essere espresso come
V = (96 – 2x) (36 – 2x)x svolgendo
V = (3.4456 – 192x – 72x + 4x2)x quindi
V = (3.4456x – 264x2 + 4x3)
e questa è la funzione che vogliamo massimizzare, perciò determiniamo la derivata rispetto a x e la uguagliamo a zero.
dV/dx = 12x2 – 528x + 3.456 = 0.
Ora, svolgendo l’equazione di secondo grado avremo risultati: 8 cm e 36 cm. Il risultato 36 non è possibile perché uguale alla lunghezza di un lato del foglio di zinco, quindi il risultato accettabile è 8 cm. Ma questo valore è un valore massimo o minimo locale? Per scoprirlo calcoliamo la derivata seconda per x = 8.
dV2/dx2 = 24x – 528 = 192 – 528 = – 336
Il risultato è minore di zero quindi x = 8 è un massimo. A conferma del calcolo precedente, il volume massimo è 80 per 20 per 8 = 12.800 cm cubi. Anche i lettori che hanno familiarità con il calcolo infinitesimale, apprezzeranno quanto sia più semplice risolvere il problema utilizzando la formula proposta da Dudeney.
I Giochi del Lunedì tornano tra due settimane.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).