
Giochi del Lunedì di Prisma del 4 novembre 2024 a cura di Fabio Ciuffoli
Oggi proponiamo tre interessanti problemi, apparentemente complicati, ma che si possono risolvere con un’intuizione sorprendentemente semplice mediante l’utilizzo di un’agevole regola o di una comoda formula. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le nostre proposte di soluzione.
Una tubazione e due cisterne
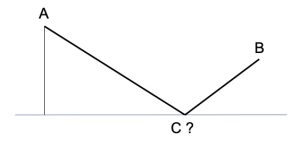
1. Un idraulico deve portare acqua attraverso un tubo dal punto A a un generico punto C che sei trova sul bordo di un deserto e poi dal punto C al punto B, come schematizzato in figura. Vengono date le dimensioni tra A e B e la distanza tra A e il confine del deserto. Dove dovrebbe essere posizionato il punto C, al bordo del deserto, in modo che la misura del tubo sia la più corta possibile?
Ci sono molti problemi di questo tipo che possono essere risolti senza usare il calcolo infinitesimale. Infatti, con una piccola intuizione si può “vedere” la soluzione.
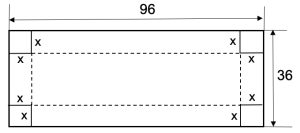
3. In questo caso l’idraulico dispone di un foglio di zinco rettangolare che misura 96 cm per 36 cm, come disegnato in figura. Ancora una volta, si desidera tagliare i quattro quadrati uguali agli angoli del foglio per ottenere una cisterna con il coperchio aperto. Quanto deve misurare il lato x dei quattro quadrati agli angoli se si vuole realizzare una cisterna a cielo aperto che contenga il massimo volume?
Aggiornamento per le soluzioni click qui.
I problemi sono tratti dal libro The call of coincidence di Owen O’Shea, Prometheus Book, Lanhan MD, 2023.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
10 risposte
Problema 3. M è il massimo entro i limiti della x. Vedi grafico
2. x=20cm ⬅️soluz
capacità cisterna=y
y=x(120-2x)²=4x(60-x)²
La cubica y ci interessa solo per x: 0<x0 e y=0 agli estremi. Quindi, stante la derivabilità di y, il suo max si troverà qnd y’=0 all’interno dell’intervallo.
y’=4[(60-x)²-2x(60-x)]=
=4(60-x)(60-3x)
Il valore che c’interessa è x: 60=3x => x=20 cvd
💪🏻🥳🏳️🌈🌈🌈
Problema 1. Il punto C va posizionato in modo che i segmenti AC e BC formino lo stesso angolo con la linea del deserto. Si dimostra che il percorso è il più corto posizionando un punto D sul prolungamento del segmento AC (ma anche BC) ottenendo il segmento AD che è esattamente la somma di AC+CB. Si può notare che qualunque percorso alternativo che punta su C’ oppure su C” è più lungo, in quanto definisce un triangolo (AC’B oppure AC”B) e si sa che nei triangoli la somma di due lati è sempre maggiore del terzo lato. Vedi immagine allegata.
Una soluzione alternativa per il 2. Il volume è V=b(a-2b)², ma prendiamo 4V=4b(a-2b)².
Questo non altera la massimalità.
Sappiamo che 4b+a-2b+a-2b=2a=costante e quindi il prodotto è massimo quando 4b=a-2b, ovvero quando b=a/6.
A conferma se studiamo V(b)=b(a-2b)² per 0<=b<=a/2 si ottiene effettivamente un massimo in b=a/6.
nei tuoi passaggi a corrisponde a 120 cm, mentre b corrisponde a x.
Problema 2 Vedi allegato
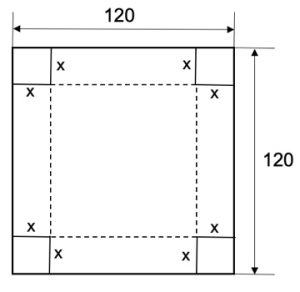
N. 2. Area di base (120-2x)² , altezza x , volume V(x) = x(120 – 2x)² = x(120² – 240x + 4x²) =
4x³ – 240x² + 120²x
Massimo per V'(x) = 12x² – 960x + 120² =1 2(x² – 80x + 1200) = 0
2x = 80 +- √(6400-4800) = 80 +- 40
Avendosi. X1=20 e X2=60 si nota che X2 comporta superficie di base nulla (120 – 2*60) e il massimo si avrà per x = 20.
Problema 3.
V = (96 – 2x)*(36 -2x)*x
V = 4x³ – 264x² + 3456x
dV/dx = 12x² -528x + 3456 = 0
x1 = 36 e x2 = 8 (correta)
V = 12800 cm²
1. Se non ho capito male il problema, è sufficiente individuare il punto B’ speculare di B rispetto alla linea blu, quindi congiungere A e B’. C è l’intersezione tra quest’ultimo segmento e la linea blu.
2. x che massimizza x(120-2x)^2, x = 20 cm
3. x che massimizza x(96-2x)(36-2x), x = 8 cm
Giorgio, perfetto come sempre. A domani pomeriggio per le soluzioni argomentate.