133. Soluzioni del 7 ottobre 2024 – Pensa due volte!

Soluzioni del 7 ottobre 2024 a cura di Fabio Ciuffoli

Ieri abbiamo presentato cinque problemi tratti dal nuovo libro di Alex Bellos, Think Twice e di seguito pubblichiamo le soluzioni. 

Pensa due volte! – soluzioni 

1. E’ maggiore la  misura dell’altezza di questo bicchiere tradizionale da pinta, oppure la misura della circonferenza del bordo superiore?

L’effetto sorprendente vale anche per il bicchiere Peroni, molto sottile e allungato come si vede in figura, che ha un diametro di 7,6 cm, quindi una circonferenza di 23,8 cm e un’altezza di soli 23,1 cm. Sembra davvero incredibile, eppure anche dopo aver misurato la circonferenza e l’altezza del bicchiere stentiamo a crederlo, come se la visione fosse in contrasto con la ragione calcolante. Morale: gli esseri umani hanno molte difficoltà a stimare la lunghezza delle circonferenze. Siamo abituati a misurare le linee rette e quando siamo di fronte a un bicchiere, guardiamo da sinistra a destra e di nuovo indietro, ma la circonferenza non è il doppio del diametro, è più di tre volte più lunga!

2. Giacomo sta guardando Anna e Anna sta guardando Giorgio. Giacomo è sposato e Giorgio non è sposato. Una persona sposata guarda una persona non sposata?
a. Sì                                                b. No                                         c. Non è possibile determinarlo

2. SOLUZIONE. Non conosciamo lo stato civile di Anna, potrebbe essere sposata o non sposata. Se fosse sposata, allora una persona sposata (Anna) sta guardando una persona non sposata (Giorgio). Se non fosse sposata, una persona sposata (Giacomo) sta guardando una persona non sposata (Anna). Possiamo dedurre che, qualunque sia lo stato civile di Anna, una persona sposata sta guardando una persona non sposata, quindi la risposta corretta è a.  Questo problema fu scritto da Hector Levesque, professore di Informatica dell’Università di Toronto, e ha suscitato molte discussioni negli studi di psicologia. Quando viene presentato con due sole opzioni (a. sì oppure b. no) le persone sono costrette a pensare allo stato civile di Anna e probabilmente otterranno la risposta corretta, ma quando c’è una terza opzione, che suggerisce che non è possibile determinarlo, il nostro cervello sceglie la via più semplice. Siamo facilmente attratti dalla possibilità di non avere informazioni sufficienti per risolvere il problema e quindi ci asteniamo dal ragionare in modo impegnativo. Forse perché provare a ragionare partendo da una “quantità sconosciuta”, in questo caso lo stato civile di Anne, è cognitivamente difficile. La possibilità di non dover pensare è troppo allettante. La morale è che anche se una quantità è sconosciuta, potremmo comunque usarla per dedurre fatti dimostrabili. Occorre solo un momento di riflessione e di pensiero ulteriore.

3. Un concorrente può scegliere tra i due Ruote della Fortuna: se gira la Ruota A, ha il 50% di possibilità di vincere, mentre se gira la ruota B, la probabilità di vincita è del 25%. Se ottiene almeno una volta Win, vincerà 1 milione. Quale delle seguenti tre opzioni dà la maggiore probabilità di vincita?

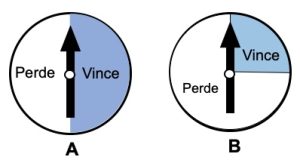
a. Girare A una volta                        b. Girare B due volte                         c. Non fa differenza

3. SOLUZIONE. La migliore opzione è a. Girare A una volta. Molte persone pensano che l’opzione b, con due giri, dia maggiori possibilità di vincita, ma in realtà non è così. Se viene girata A una volta, si ha una probabilità di ½ o del 50% di vincere. Se viene girata B una volta, si ha 1/4, o il 25% di probabilità di vincere e 3/4 o il 75% di perdere. Se viene girata B due volte, si ha probabilità di (¾ • ¾) pari al 56,25% di perdere entrambe le volte, perché la probabilità che si verifichino due eventi indipendenti è data dal prodotto delle loro probabilità. Il 56,25% di probabilità di perdere equivale al 43,75% di vincere, quindi è meglio l’opzione a. Girare A una volta, che dà il 50% di probabilità di vincita. Non è sempre così nella vita, ma nelle scommesse di questo tipo si dice che è meglio “mettere tutte le uova nello stesso paniere”.

• a. La linea curva grigia è più lunga;
• b. La linea curva nera è più lunga;
• c. Le linee curve grigia e nera hanno la stessa lunghezza;
• d. Non ci sono informazioni sufficienti per determinare la relativa lunghezza delle linee.

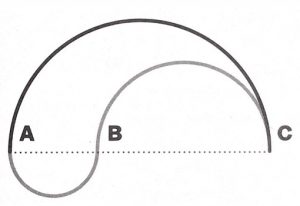
4. SOLUZIONE. L’affermazione vera è la c. Il problema ha fatto parte del SAT Test per l’ammissione all’università americana ed è uno di quelli che molte persone tendono a sbagliare. Indichiamo con x la lunghezza AC e con y la lunghezza AB quindi BC = x – y.La lunghezza del semicerchio nero AC è πx/2; la lunghezza del semicerchio grigio piccolo AB è πy/2;  la lunghezza del semicerchio grigio grande BC è  π(x – y)/2 = (πx/2) – (πy/2). La lunghezza totale delle linee curve grigie è (πy/2) + (πx/2) – (πy/2) = πx/2. Pertanto, sia la linea nera che quella grigia hanno la stessa lunghezza. Si noti che la dimostrazione non richiede alcuna lunghezza determinata. Infatti, qualunque sia la posizione relativa di A, B e C, le linee curve nere e grigie misurano la stessa lunghezza.  

5.  Quale teiera contiene più tè quando è piena?

5. SOLUZIONE. La teiera più bassa a sinistra contiene più tè perché ha un beccuccio più alto. Il livello del tè non può mai superare il livello del beccuccio, altrimenti traboccherebbe. Tuttavia, se in qualche modo bloccassimo i beccucci, la teiera più alta potrebbe contenere più tè a causa del maggior volume. Per sfruttare una qualsiasi caraffa alta, con beccuccio basso, potremmo installare una camera interna con bocca alta in prossimità del beccuccio, come illustrato sotto. In questo modo il liquido, nella sezione principale della caraffa, si riempirà fino all’altezza della bocca della camera.

I problemi sono tratti dal nuovo libro di Alex Bellos “Think Twice – Solve the simple puzzles (almost) every one gets wrong” uscito nel settembre 2024.