
I Giochi del Lunedì di Prisma del 7 ottobre 2024 a cura di Fabio Ciuffoli
Oggi presentiamo cinque problemi proposti dall’amico Alex Bellos, noto columnist di The Guardian, che ha raccolto una serie di enigmi contro-intuitivi nei quali la risposta ovvia non è quella corretta. Attenzione, non fidatevi troppo perché potremmo bluffare ancor a una volta! Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le soluzioni commentate.
Pensa due volte!
1. E’ maggiore la misura dell’altezza di questo bicchiere tradizionale da pinta, oppure la misura della circonferenza del bordo superiore?

2. Giacomo sta guardando Anna e Anna sta guardando Giorgio. Giacomo è sposato e Giorgio non è sposato. Una persona sposata guarda una persona non sposata?
a. Sì b. No c. Non è possibile determinarlo
3. Un concorrente può scegliere tra i due Ruote della Fortuna: se gira la Ruota A, ha il 50% di possibilità di vincere, mentre se gira la ruota B, la probabilità di vincita è del 25%. Se ottiene almeno una volta Win, vincerà 1 milione. Quale delle seguenti tre opzioni dà la maggiore probabilità di vincita?
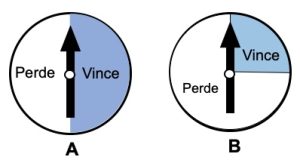
a. Girare A una volta b. Girare B due volte c. Non fa differenza
4. Nell’immagine seguente, la linea curva grigia è composta da un semicerchio che unisce A a B e un semicerchio che unisce B a C. Un semicerchio nero unisce A a C. Quale delle seguenti affermazioni è vera?
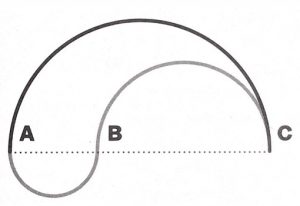
5. Quale teiera contiene più tè quando è piena?

Aggiornamento per le soluzioni click qui.
I problemi sono tratti dal nuovo libro di Alex Bellos “Think Twice – Solve the simple puzzles (almost) every one gets wrong” uscito nel settembre 2024.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
11 risposte
n. 4. Nera e grigia hanno la stessa lunghezza essendo il diametro della semicirconferenza nera = alla somma dei due diametri delle due semicirconferenze grigie.
2. Sì. Se Anna non è sposata, allora è vero l’assunto.
Se invece Anna è sposata, allora Anna (sposata) sta guardando Giorgio (non sposato). L’assunto è vero nuovamente.
N. 4 – C stesso diametro!
Sui Problemi 1 e 5 mi butto, senza pensarci due volte!
…e quindi sbaglierò 🙂
1.
Non ci sono informazioni sufficienti per rispondere, ma a naso direi che la circonferenza è superiore all’altezza.
5.
Guardando semplicemente l’immagine verrebbe da dire che la prima a sx abbia una capacità maggiore, ma osservando meglio il becco di uscita, notiamo che la seconda ha il foro di uscita più in alto, quindi potrà contenere più liquido al suo interno.
Buongiorno Vic, sulla 1 va detto che la foto del bicchiere è reale quindi si possono mettere in relazione le misure del diametro del bordo superiore e l’altezza del bicchiere. Ad esempio sul monitor del mio computer il diametro è circa 6 cm, mentre l’altezza è circa 11 cm. A domani per le soluzioni commentate.
Ciao Fabio.
Perfetto, se ci riferiamo allora esattamente al bicchiere in foto, riprodotto in scala, confermo quindi la mia risposta.
L’altezza infatti è ben inferiore a tre volte il diametro!
Problema 2.
La risposta è
a. Sì
Ragionando semplicemente in termini binari (una persona è sposata OPPURE non è sposata), risulta che sicuramente “Una persona sposata guarda una persona non sposata”.
Infatti, pur non sapendo nulla sullo stato civile di Anna:
– se Anna è sposata => Lei guarda Giorgio => OK
– se Anna non è sposata => Giacomo guarda lei => OK
Tertium non datur.
AC = 2r
AB = 2x
BC = 2r – 2x
L(AC) = πr
L(AB) = πx
L(BC)= π(r-x)
L(AB+BC) = π(x+r-x) = πr =L(AC)
Problema 3.
A -> 50%
B -> 1- (0,75*0,75)=43,75%
quindi a.
Ruote della fortuna
Confrontiamo le probabilità:
• Girare la ruota A una volta dà una probabilità di vincita del 50%.
• Girare la ruota B due volte dà una probabilità di vincita del 43.75%.
Pertanto, la risposta corretta è:
a) Girare la ruota A una volta
Problema 4
AB=a
BC=b
Linea curva nera = pi greco•(a+b)
Linea curva grigia = pi greco• a + pi greco • b= pi greco•(a+b)
Quindi hanno la stessa lunghezza.