
I Giochi del Lunedì di Prisma del 21 ottobre 2024 a cura di Fabio Ciuffoli
Oggi presentiamo tre problemi di matematica applicata tratti da New Scientist, importante rivista settimanale britannica di divulgazione scientifica. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le soluzioni commentate.
Fiori, grattacieli e banchine
1. Il deposito di fiori. Le strade di una città sono disposte secondo una griglia rettangolare come disegnato in figura.
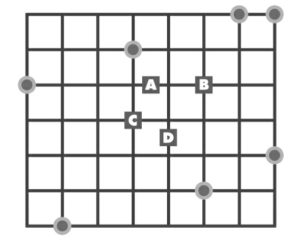
Sette fiorai, indicati dai cerchi, gestiscono le loro bancarelle nelle stazioni della metropolitana e vogliono allestire un deposito centrale da dove poter ritirare i fiori ogni mattina. Vogliono mantenere al minimo la distanza combinata dalle bancarelle al deposito. Paolo ha selezionato quattro luoghi possibili: A, B, C e D. Sandro chiede: “Sei sicuro che una di queste quattro sia la posizione ottimale? Suppongo che dovremmo verificare la distanza totale fioraio-deposito per ogni punto della griglia”. Interviene Carla: “Non è necessario, posso dirti con sicurezza la posizione migliore semplicemente guardando il diagramma”. Quale luogo consiglia Carla e perché è così sicura?
2. L’elettricista. Un alto grattacielo viene ricablato. Ci sono quattro fili che entrano in un tubo e vanno dal piano terra all’ultimo piano. I fili sono assolutamente identici, è impossibile districarli e distinguerli. L’elettricista ha pensato a un modo per individuarli: inizia dal piano terra, collegando due fili insieme (ad esempio A e C) poi si reca all’ultimo piano a piedi, perché l’ascensore è fuori uso, e mediante un tester (strumento che rileva i collegamenti tra i cavi) prova quali sono i due fili che formano un circuito elettrico, ad esempio 1 e 3. Qual è il numero minimo di salite e discese delle scale, che l’elettricista dovrà compiere per contrassegnare correttamente i quattro i cavi?

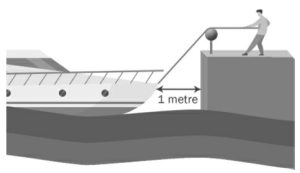
3. La barca in porto. Una barca viene legata tramite una corda a una banchina e quando la corda è tesa la barca dista 1 metro dalla banchina, come disegnato in figura. E’ in arrivo una tempesta e il marinaio, nel tentativo di evitare l’urto tra la barca e la banchina, decide di tirare la corda orizzontalmente di un metro, perciò la barca si muoverà orizzontalmente. La barca raggiungerà la banchina oppure no?
Aggiornamento per le soluzioni click qui.
I problemi sono tratti del libro Headscratcher – The puzzle book di R. Eastaway e B. Hobbs (2023).
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
12 risposte
Problema 1. Le distanze totali sono la somma delle distanze orizzontali e verticali (dato che si devono muovere sulla griglia, ho supposto). Quindi devo minimizzare lo spostamento lungo la x e lungo la y. Questo spostamento viene minimizzato se mi pongo sulla mediana della x e sulla mediana della y. Tale punto è B.
Sarò sciocco, ma lo vedo come un semplice calcolo di baricentro delle masse (tutte poste uguali a 1), in un sistema di riferimento cartesiano con origine in basso a sinistra e assi normalmente orientati:
Ʃx/n=(0+1+3+5+6+7+7)/7=29/7≈4.1
Ʃy/n=(4+0+5+1+6+2+6)/7=24/7≈3.4
Vada per D, ma un lato più in alto.
Secondo me.
3 quesito: si! Se è talmente forte da sollevare la prua della barca dal suo galleggiamento.
Per il 2°quesito: etichetto i capi dei fili in basso A, B, C, D, collego AB, salgo (1 volta) ed etichetto i capi dei fili E, F, G, H, testo e trovo corto tra E ed F, quindi ci sono le 2 possibilità A=E con B=F oppure A=F con B=E.
Scendo (2 volta) collego AC, salgo (3 volta) e trovo E corto G, quindi E=A con C=G, di conseguenza B=F, D=H.
Distanza percorsa 3 volte.
Buongiorno, mi sembra non necessaria la terza volta (salita). Si può risolvere con una salita e una discesa. Nel pomeriggio le soluzioni.
Detto O(0; 0), il vertice in basso a sinistra, l’origine del piano cartesiano, il punto deposito comune cercato sarà in G(29/7; 28/7), G=baricentro dei punti di vendita.
A domani per le soluzioni commentate
Ottimo Giorgio, come sempre. A domani per tt le soluzioni.
Problema 2.
Dovrebbero bastare due “giri”. Collego 1 e 2 e verifico che ad esempio sono associati a C e D. Torno su e collego 1 e 3. Questi saranno associati a Cx o Dx, supponiamo CA, potrò dedurre che 1C, 3A, 2D, 4B.
Problema 3. No. La raggiungerebbe solo se h = 0.
A parte il fatto che con mare mosso la barca andrebbe allontanata dalla banchina. In ogni caso dalla figura si vede che la cima è l’ipotenusa di un triangolo rettangolo, quindi accorciandola di un metro il cateto si accorcia meno di un metro.
Sia a=dislivello banchina-barca: se a=0 ===> sì, raggiunge; se a>0 ===> non raggiunge.