
Soluzione del 23 settembre 2024 a cura di Fabio Ciuffoli
Ieri abbiamo presentiamo tre problemi di geometria tratti dai Mathematical Puzzles della rivista australiana Parabola e di seguito pubblichiamo le soluzioni.
Ragionare sui rettangoli – soluzioni
1. Un foglio di carta A4 ha proporzioni 1:√2. Supponiamo che un lato sia bianco e l’altro sia blu. Il foglio viene appoggiato su un tavolo con il lato bianco rivolto verso l’alto e l’angolo A viene ripiegato, come mostrato in figura, in modo che A, E, C siano collineari e la lunghezza MN sia uguale a AD.
1.1. Quale proporzione della figura visibile MNBCD è blu?
1.2. E un’altra domanda: qual è potrebbe essere una buona ragione perché un foglio A4 abbia proporzioni 1:√2?
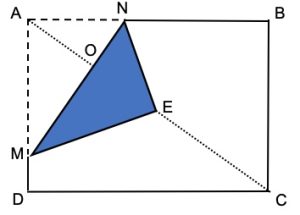
MN/AC =AD/AC=1/√3
perciò il rapporto tra le aree è (area MAN)/(area ABC) = 1/3.
1.2. In generale, quando i lati di un rettangolo hanno un rapporto 1:√2 può essere diviso a metà in due rettangoli più piccoli che avranno le stesse proporzioni. Il formato AO rappresenta il metro per definire tutti gli altri formati e corrisponde a un metro quadrato di carta, ovvero un rettangolo con lati 84,1 cm e 118,9 cm. Tagliando a metà il lato lungo di un foglio AO si ottengono fogli più piccoli, i cosiddetti A1 (misure: 84,1 x 59,4 cm) che sono esattamente la metà del formato precedente. Continuando a tagliare lungo il lato maggiore dei vari fogli si otterranno i formati A2, A3 e, appunto, A4.
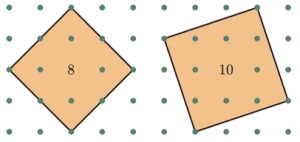
2. Su una tavola di legno sono disposti vari pioli che formano una griglia rettangolare. Attorno ai pioli è possibile posizionare degli elastici in modo da definire forme geometriche. Ad esempio, in figura viene riprodotto un particolare dove sono stati costruiti due quadrati di aree 1 e 5, utilizzando elastici fissati ai relativi pioli. Come è possibile costruire i quadrati di area 8 e di area 10?
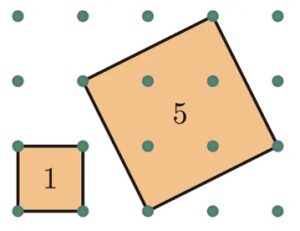
2. SOLUZIONE. Si utilizza il teorema di Pitagora, considerando che i lati del quadrato sono le ipotenuse dei triangoli rettangoli. Il quadrato di area 8 avrà il lato, corrispondente all’ipotenusa del triangolo rettangolo, l2 = 22 + 22 per cui l = √8 infine l’area sarà l2 = 8. La stessa procedura si utilizza per trovare il lato del quadrato con area 10, quindi l2 = 32 + 12 per cui l = √10 e infine l2 = 10.
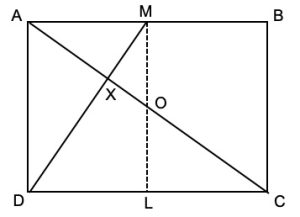
3. Nel rettangolo ABCD il punto M divide a metà il lato AB, come disegnato in figura. Calcolare il rapporto tra l’area del triangolo AXM e l’area del rettangolo ABCD.
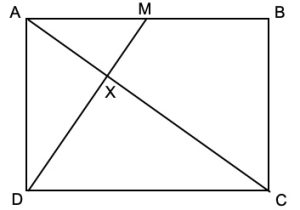
3. SOLUZIONE. Nella figura seguente indichiamo con L il punto medio del lato CD e con O il centro del rettangolo. Per semplicità indichiamo con a l’area del rettangolo ABCD. Ora i triangoli ADX e MOX sono simili poiché hanno angoli uguali in X e angoli uguali XAD e XOM, inoltre MO è metà di AD, perciò Area (ADX) = 4 Area (MOX).Area (AMX) = Area (ADM) – Area (ADX)
Area (AMX) = Area (ADM) – 4 Area (MOX) ma ADM è (¼)a, per cui
Area (AMX) = (¼) a – 4 [Area (AMO) – area (AMX)] ma AMO è (1/8)a, per cui
Area (AMX) = (¼) a – 4 [(1/8)a – Area (AMX)] ora svolgendo
Area (AMX) = 4 (Area (AMX) – (¼)a che diventa – 3 Area (AMX) = – (¼)a
Infine Area (AMX) = [(1/4)a]/3 = (1/12)a.
I Giochi del Lunedì di Prisma tornano tra due settimane.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).