
I Giochi del Lunedì di Prisma del 23 settembre 2024 a cura di Fabio Ciuffoli
Oggi presentiamo tre problemi di geometria che hanno fatto parte dei Mathematical Puzzles della rivista australiana Parabola. Ian Stewart la descrisse così: “Parabola intrattiene i suoi lettori con articoli, sondaggi e problemi di matematica volti a incoraggiare gli studenti di matematica delle scuole medie superiori… La parola chiave non è ‘matematica’ ma ‘intrattenimento’”. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio relativo ai commenti. Domani alle ore 17.00 pubblicheremo le soluzioni.
Ragionare sui rettangoli
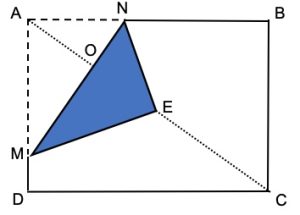
1. Un foglio di carta A4 ha proporzioni 1:√2. Supponiamo che un lato sia bianco e l’altro sia blu. Il foglio viene appoggiato su un tavolo con il lato bianco rivolto verso l’alto e l’angolo A viene ripiegato, come mostrato in figura, in modo che A, E, C siano collineari e la lunghezza MN sia uguale a AD.
1.1. Quale proporzione della figura visibile MNBCD è blu?
1.2. E un’altra domanda: qual è potrebbe essere una buona ragione perché un foglio A4 abbia proporzioni 1:√2?
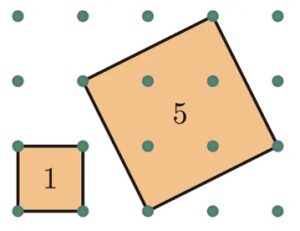
2. Su una tavola di legno sono disposti vari pioli che formano una griglia rettangolare. Attorno ai pioli è possibile posizionare degli elastici in modo da definire forme geometriche. Ad esempio, in figura viene riprodotto un particolare dove sono stati costruiti due quadrati di aree 1 e 5, utilizzando elastici fissati ai relativi pioli. Come è possibile costruire i quadrati di area 8 e di area 10?
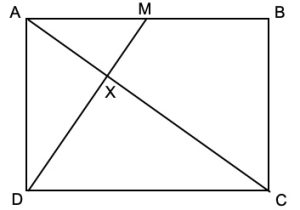
3. Nel rettangolo ABCD il punto M divide a metà il lato AB, come disegnato in figura. Calcolare il rapporto tra l’area del triangolo AXM e l’area del rettangolo ABCD.
I problemi sono tratti dal libro Parabolic Problems – 60 Years of Mathematical Puzzles in Parabola, di D. Angell e T. Britz (2024).
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
16 risposte
Problema 3
Perfetto, nel pomeriggio le soluzioni commentate.
Problema 2
Problema 1
Problema 3. Soluzione – vedi immagine
Indichiamo con u la semibase e v l’altezza del rettangolo di area r:=2vu. Siano a,b,c,d le aree in figura colorate rispettivamente in azzurro, giallo, verde e marrone. Il rapporto richiesto è s:=a/r.
Si nota che il triangolo di area a è simile a quello di area c e poiché le aree di triangoli simili stanno tra loro come i quadrati di due lati omologhi si ha a/c=u^2/(2u)^2=1/4, inoltre si vede che a+b=r/2, d+c=r/2, a+d=r/4, a+c+b+d=r con questo abbiamo un sistema di 5 equazioni lineari in 5 incognite che, per a diverso da 0, porta alla soluzione: b=5a, c=4a, d=2a, r=12a. In conclusione s=1/12.
Problema 3 Vedi immagine
Problema 1 Vedi immagine
La 1.2 rispondo subito: in questo rapporto sono rispettate le proporzioni tra le varie misure dei fogli. Dal A0 basta tagliare a metà i successivi fogli per ottenere i formati che conosciamo e usiamo, dal A1 al A6. Tale soluzione fu studiata apposta per risparmiare sulla linea di produzione. Precisazione: non è la sezione aurea (1.61…), in quanto √2 = 1,141.
Problema 1 due soluzioni allegate.
idem
Problema 1. Con un riferimento cartesiano con origine in D , posto B(a,b) con l’intersezione delle rette DM e AC rispettivamente di equazioni: y = 2.b.x/a e y = -b.x/a+b si ha X(a/3;2.b/3) per cui : S(AXM)=a.b/12 e il rapporto R=1/12.
Scusate, Problema 3.
3. Area(AXM) = 1
Area(ABCD) = S
S = S/4 + 4 + S/4-1 + S/4
S = 12
rapporto = 1/12
Ottimo, Giorgio come sempre ineccepibile e preciso. A domani per le soluzioni commentate.
1. AMN simile ad ACD
AD = 1
x^2 + y^2 = 1
y : x = sqrt(2) : 1
x = 1/sqrt(3)
y = sqrt(2/3)
area(AMN) = area(MNE) = 1/(3sqrt(2))
area(MNE)/area(ABCD) = 1/6
area(MNE)/area(MNBCD) = 1/5
Problema 2. Vedi disegno allegato