
I Giochi del Lunedì di Prisma del 15 luglio 2024 a cura di Fabio Ciuffoli
Esiste un istinto matematico negli animali? Molte ricerche hanno dimostrato l’esistenza di una matematica istintiva di cui si servono molti animali tra i quali i cani, gatti, gufi, castori, ragni, aragoste ed altri. Essi “sanno fare matematica”, escogitare trucchi e scoprire strategie per sopravvivere, migliorare le loro capacità intuitive e risolvere problemi. Prendendo spunto da queste considerazioni, presentiamo due problemi. Nel primo, riproponiamo il sorprendente esperimento condotto da Tim Pennings, professore di Matematica al Hope College del Michigan, sull’intelligenza matematica dei cani “Do dogs know calculus?”. La soluzione, che il cane trova istintivamente, è abbastanza complessa e richiede l’impiego del calcolo infinitesimale. Nel secondo problema, simile al primo, trattiamo l’ottimizzazione vincolata in cui si chiede di minimizzare il costo di trasporto. Invitiamo i lettori a inviarci osservazione e proposte di soluzione utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le soluzioni.
L’istinto matematico
1. Il cane all’inseguimento della pallina Un cane e il suo padrone stanno giocando sulla riva di un lago. Il padrone lancia una pallina nell’acqua ed il cane va a recuperarla. Se il lancio è dritto davanti a sé, il cane si butta nel lago e nuota direttamente verso la pallina. Se il lancio è in diagonale, rispetto al punto dove si trova il cane sulla spiaggia, allora il cane, invece di buttarsi direttamente verso la pallina, corre lungo la riva per un po’ prima di tuffarsi in acqua e poi nuotare fino alla pallina. Il cane vuole recuperare la pallina nel minor tempo possibile. Dal momento che esso può muoversi molto più velocemente sulla terraferma di quanto lo possa fare nuotando in acqua, la via più veloce è correre lungo la riva per un tratto e poi tuffarsi e nuotare per il tratto rimanente.
Schematizzando, con il disegno in figura, la pallina lanciata si trova in B e il cane in A. Il cane corre lungo la riva fino al punto D e poi si getta in acqua e nuota in direzione di B. Supponiamo che BC sia 10 metri, AC sia 20 metri e che la velocità del cane a terra sia 4 volte maggiore della sua velocità in acqua, si chiede di calcolare la distanza AD che il cane percorre a riva prima di tuffarsi in acqua al fine di minimizzare il tempo per raggiungere B?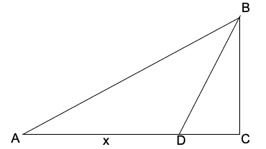
2. Strada sterrata o sabbiosa. Un’automobile fuoristrada deve andare dal punto A al punto B con le distanze rappresentate in figura. Deve attraversare, inizialmente, un tratto sterrato con un consumo di carburante 0,25 litri al km e poi un tratto sabbioso con consumo di carburante 0,5 litri al km. Individuare il percorso che minimizza il consumo di carburante e calcolare il consumo totale di carburante.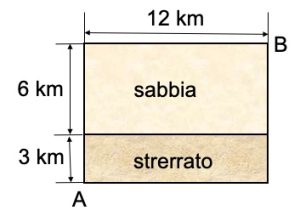
Aggiornamento per le soluzioni click qui.
Il primo problema è tratto dal libro L’istinto matematico di Keith Devlin. Il secondo problema è stato proposto da Carmelo Giugno, che ringraziamo per il contributo, in un social media di divulgazione matematica. Un problema simile, denominato Problema del Bagnino, è stato spesso utilizzato e forse inventato da Richard Feynman premio Nobel per la fisica del 1985.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
13 risposte
Strada sterrata o sabbiosa.
Indicando con L1 e L2 i percorsi nello sterrato e nella sabbia e con θ1 e θ2 gli angoli con la normale si ottiene:
L1sen( θ1) +L2 sen ( θ2)=12
L1cos( θ1)=3
L2 cos( θ2)=6
sen( θ1)=2sen ( θ2) (legge di Snell)
Da cui θ1=71,131°, θ2=28,238°, L1=9,276Km, L2=6,810Km, consumo minimo=5,724 litri
Vedi immagine
Per quanto riguarda il problema del cane e la pallina, si richiede il percorso riva acqua che minimizza il tempo.
Sia f la funzione tempo che dipende dal tratto percorso sulla riva (da (0;0) a (x;0))
e nell’acqua in diagonale da (x;0) a (20;10)
f(x) = x/4+sqrt((20-x)^2+10^2)
f'(x) = 1/4-(20-x)/sqrt((20-x)^2+10^2)
Ponendo f'(x)=0 si trova che f(x) è minimo per x = 17,418
da cui f(17,418) = 14.6825 unità di tempo che dipendono dalla velocità del cane
Sullo sterrato il consumo è
c₁=1/4 l/km
sulla sabbia è
c₂=1/2 l/km
deve esistere una distanza orizzontale x per l′interfaccia tra i due mezzi per cui il consumo è minimo e i percorsi devono essere rettilinei
L₁=√(x²+3²), L₂=√((12-x)²+6²)
C(x)=L₁/4+L₂/2
C(x)=√(x²+3²)/4+√((12-x)²+6²)/2
dC(x)/dx=0
fornisce
x(min)≈8.777745
L(x(min))≈16.09675 km
C(x(min))≈5.7243 l
vedi disegno
Va trovato il valore di x che rende minimo: sqrt(x^2+3^2)*.25 + sqrt((12-x)^2+6^2)*.5.
x = ~8.77775 km
percorso totale: ~16,08675 km
consumo totale: ~5.72431 litri.
Problema dello sterrato e della sabbia – Per chi ha risposto 6,09 l, provate a fare una diagonale un po’ più corta nello sterrato e vedrete che avrete un consumo inferiore. Il consumo minino si ottiene con una diagonale di 9,28 km circa sullo sterrato e di 6,81 km circa sulla sabbia, per un consumo totale di 5,72 l
Segue la legge della rifrazione.
Strada sterrata o sabbiosa. consumo 6,09 litri
vedi immagine
Non è così. A domani per le soluzioni.
1. Il cane all’inseguimento della pallina. Va trovato x che minimizza: x + 4 * sqrt((20-x)^2 + 10^2)
x = 20 – 2 * sqrt(5/3) = ~17.418 m.
È il mio problema della spiaggia! Sto camminando sul bagnasciuga dove vado al doppio della velocità di quando cammino sulla sabbia e ho l’ombrellone piantato a N metri dal bagnasciuga. Quando devo abbandonare il bagnasciuga e puntare dritto all’ombrellone per minimizzare il tempo?😂😂
2. Non ho fa far conti con me, ma io prenderei un punto x a sul limitare, e cercherei il minimo della funzione:
0.25*Sqrt(9+X^2) + 0.5*Sqrt((12-x)^2 + 36)
A occhio, visti i consumi, è facile che la soluzione sia di minimizzare il tratto sabbioso, ma mi appoggerei alle formule più che all’intuizione.
Problema 2 – Secondo me il percorso dovrà essere una spezzata composta da 2 segmenti AC e CB, dove C è un punto sul limite tra sabbia e sterrato.
Consideriamo:
A = (Xa, Ya) = (0, 0)
B = (Xb, Yb) = (12, 9)
C = (Xc, Yc) = (X, 3)
Il consumo di benzina sarà dunque:
b(C) = 0.25×AC + 0.5×CB
b(X) = 0.25×Sqr[(X^2-Xa^2) +
+ (Yc^2-Ya^2)] +
+ 0.5×Sqr[(X^2-Xb^2) + (Yc^2-Yb^2)]
= (1/4)×Sqr[X^2 + 9] +
+ (1/2)×Sqr[X^2 – 144 + 9 – 81]
= (1/4)×Sqr(X^2 + 9) +
+ (1/4)×Sqr(X^2 – 216)
ora bisognerà individuare il minimo di questa funzione, che si dovrebbe avere quando risulta.
db(X)/dX = 0