126. Soluzioni del 1° luglio 2024 – Test ingresso Medicina e Veterinaria 2024

Soluzioni del 1° luglio 2024 a cura di Fabio Ciuffoli

Ieri abbiamo presentiamo sei domande di ‘Ragionamento logico’ tratte dai test di Medicina e Veterinaria svolti il 28 e 30 maggio 2024, di seguito pubblichiamo le nostre proposte di soluzione.

Test d’ingresso Medicina e Veterinaria 2024 – soluzioni 

1. La casa di Andrea ha un’estensione che supera di 42 metri quadri la metà della superficie complessiva delle case di Benedetto e Cesare. Indicando con A, B e C rispettivamente l’estensione in metri quadri delle case di Andrea, Benedetto e Cesare, quale delle seguenti uguaglianze è corretta?

• A) A + 42 = (B + C)/2
• B) A – 42 = (B + C)/2
• C) A = 42 + 2(B + C)
• D) A = (42 + B + C)/2
• E) A + 42 = 2(B + C)

1. SOLUZIONE. La superficie della casa di Andrea (A) è metà della somma delle superfici delle case di Benedetto (B) e Cesare (C) a cui aggiungiamo 42 metri. Perciò A – 42 = (B + C)/2. La soluzione è B.

2. Dopo la scuola, Andrea ha sempre molta fame e si ferma in una panetteria. Quando compra due focacce ripiene ed una pasta spende 8 €, quando compra una focaccia ripiena e due paste spende 7 €. Oggi ha comprato soltanto una focaccia ripiena ed una pasta, quanto ha speso?

A) 6 €               B) 4 €             C) 4,50 €         D) 5 €           E) 5,50 €

2. SOLUZIONE. Si imposta un sistema con due equazioni e due incognite, indicando focaccia con F e pasta con P, avremo

quindi Andrea ha speso 2 + 3 = 5 euro. La soluzione è D.

3. Lanciando due volte un dado a sei facce, qual è la probabilità che in almeno un lancio si ottenga un 5 o un 6?

A) 20/36        B) 24/36        C) 22/36       D) 11/36       E) 12/36

3. SOLUZIONE. In questo caso conviene calcolare la probabilità che non esca un 5 o un 6 in ciascuno dei due lanci, che è (4/6)•(4/6) = 16/36. A questo punto possiamo calcolare la probabilità complementare che è 1 – 16/36 = 20/36. La soluzione è A.

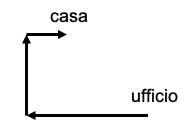
4. Per raggiugere la sua casa in macchina dall’ufficio, Diana si dirige a ovest per 3 km su Corso Italia, poi per 2 km in direzione nord si Via Vecchia, infine per 1 km in direzione est su Via Marulli, dove si trova la sua abitazione. Dal suo appartamento all’ottavo piano Diana riesce a vedere il suo ufficio. In che direzione si trova l’ufficio di Diana rispetto al suo appartamento?

A) Sud-ovest     B) Nord C) Sud        D) Nord-ovest       E) Sud-est

4. SOLUZIONE. Si può schematizzare il percorso dall’ufficio all’appartamento. Diana si sposta prima verso Ovest e poi verso Nord, poi torna verso Est, ma per una distanza inferiore. L’appartamento sarà quindi a Nord-ovest rispetto all’ufficio, quindi l’ufficio sarà a Sud-est rispetto all’appartamento. Risposta corretta è la E.

5. In un sistema di assi cartesiani ortogonali e monometrici con origine O, si consideri la retta r di equazione y = -x + 2. Siano A e B i punti di intersezione di r con l’asse delle ordinate e con l’asse delle ascisse, rispettivamente. Quanto vale l’area del triangolo di vertici AOB?

A) 4       B) 2        C) 3       D) 5        E) 1

5. SOLUZIONE. Si tratta di un triangolo rettangolo, uno dei due cateti ha lunghezza 2, poiché l’intercetta q = 2, andando a sostituire con x = 2 avremo y = 0 quindi anche l’altro cateto ha lunghezza 2, perciò l’area del triangolo è (2•2)/2 = 2. La risposta corretta è B.

6. Tutti gli innamorati sono felici. Chi è felice sorride. Roberto è felice. Se le precedenti osservazioni sono vere, quale delle seguenti deduzioni è certamente non corretta?

• A) Chi è innamorato sorride.
• B) Roberto sorride.
• C) Chi è felice è innamorato.
• D) Roberto è felice.
• E) Non è detto che Roberto sia innamorato.

6. SOLUZIONI. La affermazioni proposte si possono schematizzare con tre insiemi. L’insieme degli ‘innamorati’ è compreso all’interno dell’insieme delle persone ‘felici’, che a sua volta è contenuto all’interno dell’insieme delle persone che ‘sorridono’. L’unica risposta non deducibile con certezza è: “Chi è felice è innamorato” perché l’insieme delle persone innamorate si trova all’interno di quelle felici , quindi non necessariamente una persona felice è innamorata. La risposta corretta è la C.

I Giochi del Lunedì tornano tra due settimane.