I Giochi del Lunedì di Prisma del 22 aprile 2024 a cura di Fabio Ciuffoli
Presentiamo tre giochi matematici che richiamano la tradizione giapponese di appendere fuori dai templi tavolette di legno decorative con problemi di geometria. Queste immagini, chiamate sangaku, hanno valore votivo e contemplativo, fanno della matematica un evento collettivo, una fonte di intrattenimento visivo e di meraviglia. La loro composizione, armoniosa e artistica, riporta prevalentemente disegni con iscrizioni ridotte al minimo: un vero e proprio un invito alla meditazione. Chiediamo ai lettori di inviarci osservazioni e proposte di soluzione, utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le nostre proposte di soluzione.
Cerchi e triangoli sangaku
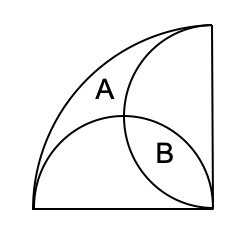
1. Ala e lente. Un quarto di cerchio contiene due semicerchi più piccoli come disegnato in figura. Dimostrare che la sagoma ad ala A ha la stessa area della sagoma a lente B.
2. Diciotto cerchi. L’immagine mostra cerchi di cinque dimensioni. Ci sono sei cerchi bianchi, sette grigio scuro, tre grigio chiaro, uno tratteggiato inscritto nel triangolo e uno più grande descritto da una linea continua. Qual è il rapporto tra il raggio del cerchio tratteggiato e il raggio di un cerchio bianco?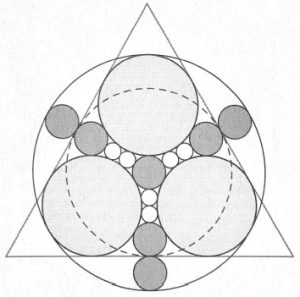
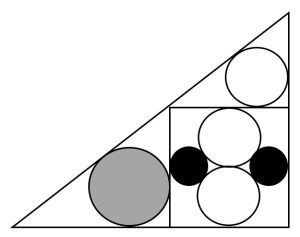
3. Sei cerchi in un triangolo. Nella figura compaiono cerchi di tre diverse dimensioni: due neri, tre bianchi e uno grigio. Due cerchi neri e due bianchi sono inscritti in un quadrato. Il quadrato, insieme ad altri due cerchi, è collocato in un triangolo rettangolo. Dimostrare che il raggio del cerchio grigio è il doppio del raggio del cerchio nero.
Aggiornamento per le soluzioni click qui.
Il primo problema è tratto da The Tokyo Puzzle di Fujimara Kobon. Il secondo è attribuito a Shigetoshi Tanabe che, a soli quindici anni, lo espose nel 1865 in un tempio a Nagoya. Il terzo è opera di un tredicenne Naosue Sato che nel 1847 lo espose in un tempio a 300 km a nord di Tokyo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
11 risposte
Riporto un interessante confronto con Raffae Scognamiglio sul problema 2. Vedi anche immagine allegata.
Fabio Ciuffoli a Raffae Scognamiglio: “La soluzione al problema 2 a me viene 10. Sono fuori casa, appena posso cerco di capire dove sta la differenza. A presto, tks per il lavoro svolto. A un primo controllo, secondo me l’ipotesi r(ct) = h(tr) (se ho capito bene il raggio del cerchio tratteggiato è uguale all’altezza del triangolo rosso) non è valida, mentre mi sembra corretta la costruzione dei due esagoni regolari rosso e blu. Attendo il tuo parere, domani ci guardo meglio. Ciaoo”.
Raffae Scognamiglio a Fabio Ciuffoli: “Sulla correttezza dell’ esagono rosso sono certa, se anche l’esagono blu è corretto, cioè, i vertici del rosso sono punti medi dei lati dell’esagono blu e, i vertici del blu appartengono all’altra circonferenza, (cioè l’esagono blu così costruito risulta inscritto proprio nella circonferenza concentrica a quella tratteggiata rappresentata nel quesito e non ad un’altra ad essa concentrica), allora il mio procedimento e i miei calcoli sono giusti.
È corretta la posizione r(c.t.)=h(t.r.)
Infatti, la circonferenza tratteggiata è inscritta nel triangolo equilatero. Io ho posto pari ad l il lato del triangolo equilatero assegnato ( mia unica ipotesi), poiché
r(c.t.)=A/p
A(t.eq.)=l²√3/4, 2p=3l->p=3l/2
da cui r(c.t.)=l√3/6 ma,
r(c.t.) apotema dell’esagono, vuol dire che a(esagono)=l√3/6
L’esagono può essere diviso in 6 triangoli equilateri la cui altezza è proprio l’apotema dell’esagono, per cui h(t.r.)=r(c.t.)=l√3/6
Mia unica ipotesi l(t.eq.assegnato)=l
Ho rifatto i calcoli a ritroso, partendo dal fatto che r(C.t.)/r(C.b.)=10 e ho trovato che
r(C.circ.esagono blu)=2z+x=7l√3/30
invece con la mia costruzione viene
r(C.circ.esagono blu)=2z+x=2l√3/9 di poco più piccolo come si può notare, per cui i vertici dell’esagono blu che ho costruito dovrebbero appartenere ad una circonferenza concentrica a quella del grafico. Dopo attenta verifica, sono certa che il problema della differenza del risultato sia proprio questo.”
Fabio Ciuffoli a Raffae Scognamiglio: “D’accordo la differenza del risultato, 10 anziché 8, implica una diversa misura del r(C.circ.esagono blu). Questo mi porta a dire che non è verificata l’ipotesi che “i vertici dell’esagono rosso sono punti medi dei lati dell’esagono blu” pur restando valida la costruzione dei due esagoni rosso e blu e la concentricità delle due circonferenze tratteggiata e di quella più grande. Grazie per il confronto.
Quesito 1. Vedi allegato disegno. B = 2C = πr^2/8 – r^2/4 = (π-2)r^2/8
A + B = A + 2C = πr^2/4 – r^2/2 = (π-2)r^2/4 =2B
A = B c.v.d.
N. 2. Indicando con b il raggio dei cerchi bianchi, con gs quello dei cerchi grigio scuro, con gc quello dei cerchi grigio chiaro, con t quello del cerchi tratteggiato e con G il raggio del cerchio più grande, possiamo scrivere le seguenti uguaglianze
gs+4b+2gs=t
gs+4b+4gs=G
gs+2gc=G
gs+4b+gs=gs+gc
Le prime tre provengono evidentemente dalla possibilità di decomporre alcuni raggi più grandi in segmenti radialie diametrali più piccoli, la quarta è un po’ più complicata da vedere e discende dal fatto che il quadrilatero che ha per vertici il centro del cerchio grigio scuro centrale, i centri di due cerchi grigio scuro lungo due direzioni diverse e il centro del cerchio grigio chiaro adiacente è un rombo e quindi ha lati uguali che possono essere decomposti nei due modi descritti. Abbiamo quindi le equazioni
4+3gs/b=t/b
4+5gs/b=G/b
gs/b+2gc/b=G/b
4+gs/b=gc/b
Risolvendo il sistema si ha t/b=10
L’area di A si ottiene sottraendo al quarto di cerchio i due semicerchi e aggiungendo B che sarebbe tolto due volte anziché una.
Ma quarto di cerchio e i due semicerchi sono equivalenti
Rimane A = B
A = (pi r^2)/4 – 2* pi(r/2)^2 /2 + B
quindi A = B
Quesito 3. vedi immagine allegata
1. Se 2r è il raggio del quarto di cerchio Q e C è l’area di ciascun semicerchio piccolo, si ha:
Q = C + C – B + A cioè
1/4(pi x (4r^2))=
= 2×1/2(pi xr^2) – B + A
e con un rapido calcolo algebrico => A = B
1.
B = 2C
Dalla proporzione lineare 1:2 si ricava che il quarto di cerchio di raggio 2 ha area quadrupla del quarto di cerchio di raggio 1, quindi A+2C = 4C, ma B = 2C, quindi A+2C = B+2C, A = B.
Bene, ottima grafica. A domani per le soluzioni commentate anche da un altro punto di vista.
3.
Ricavo r con Pitagora:
(2-r)^2 + 1 = (1+r)^2 da cui r = 2/3
Triangoli simili, ricavo x e R.
(1+x)/4 =4/(4R)
(1+x)^2+16=(3+x)^2
da cui x = 2, R = 4/3
R = 2r
Ottimo, chiaro e sintetico. A domani per la nostra proposta di soluzione.
Problema 1.
Detto R il raggio di ciascuno dei semicerchi, ne consegue che 2R è il raggio del quarto di cerchio e, pertanto, che l’area di ciascun semicerchio vale πR²/2, mentre quella del quarto di cerchio vale πR². La somma delle aree dei due semicerchi dunque equivale all’area del quarto di cerchio, per cui A e B non possono che essere equivalenti.