Menu
12. Le soluzioni del 27 settembre 2021 a cura di Fabio Ciuffoli
Nella mattinata di ieri abbiamo proposto un problema di geometria, che il primo ministro russo, Mikail Mishustin, ha illustrato durante l’inaugurazione dell’anno scolastico circa un mese fa. Ora presentiamo la soluzione.
Il Primo Ministro russo e la geometria – soluzione
Agli inizi di questo mese, il primo ministro russo Mikhail Mishustin ha celebrato il Giorno del Sapere, visitando una delle migliori scuole del suo paese nei pressi di Mosca.
Terminato il discorso inaugurale, si è avvicinato alla lavagna e ha proposto il seguente problema:
“A partire da un punto su una circonferenza, siete in grado di disegnare una perpendicolare al diametro, senza utilizzare dispositivi di misurazione?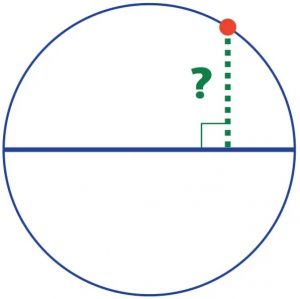
In altri termini, data una circonferenza con il suo diametro e un punto, indicato in rosso, trovate un modo per tracciare una linea passante per il punto, indicata in tratteggiato verde, che formi un angolo retto col diametro.”
La bellezza di questo problema è nella restrizione degli strumenti di misurazione. E’ permesso solo un righello, non contrassegnato, per disegnare linee rette.
La fotografia del primo ministro, in alto, fornisce qualche indizio. Ad esempio l’angolo inscritto in una semicirconferenza è retto. Alcune conoscenze sui triangoli possono essere utili: l’altezza di un triangolo è il segmento che parte da un vertice e forma un angolo retto incontrando il lato opposto; nei triangoli acuti le tre altezze si intersecano sempre.
SOLUZIONE.
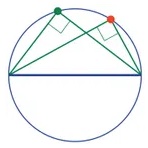
Passo 1. Tracciamo due segmenti dal punto (rosso) fino alle due estremità del diametro. Individuiamo, a scelta, un altro punto (verde) sulla circonferenza e tracciamo due segmenti fino all’estremità del diametro. Gli angoli, da entrambi questi punti, sono retti come illustrato a fianco.
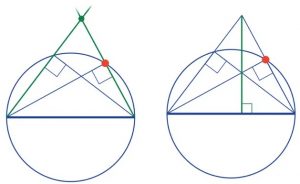Passo 2. Prolunghiamo i segmenti che attraversano entrambi i punti fino al loro incontro, individuando così il vertice di un triangolo. Due altezze di questo triangolo sono state già disegnate Sappiamo che le altezze si intersecano, perciò tracciando il segmento dal vertice più alto, passante per l’intersezione delle due altezze sottostanti, avremo la terza altezza che cadrà ortogonalmente sul diametro, come illustrato a fianco.
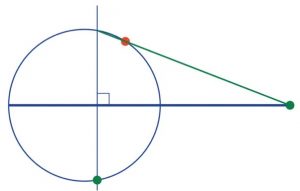
Passo 3. Ora il nostro compito è disegnare un segmento, parallelo alla terza altezza e che passi per il punto rosso. Tracciamo un segmento, passante per il punto di intersezione tra la nostra perpendicolare e la circonferenza e il punto rosso, fino a congiungersi con il prolungamento del diametro, come illustrato a fianco.
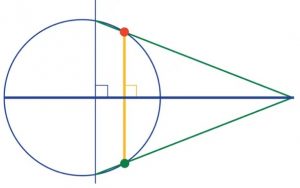Passo 4. Tracciamo un segmento dall’intersezione a destra nella figura fino all’intersezione della nostra perpendicolare con la circonferenza, nella parte inferiore del cerchio. Questa linea deve intersecare il cerchio nel punto speculare del punto rosso. La linea che li unisce è la perpendicolare che stavamo cercando come illustrato a fianco.
Ed ecco il disegno della soluzione del primo ministro russo Mishustin.
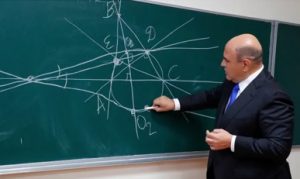
Si ringrazia l’International Congress of Mathematicians (ICM) per l’utilizzo delle immagini.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
Una risposta
Aggiungo la ottima soluzione proposta da Silvano Vallerini con Geogebra.