Menu
Soluzioni del 25 marzo 2024 a cura di Fabio Ciuffoli
Ieri abbiamo presentato quattro problemi che mettono in relazione la croce e il cerchio e abbiamo ricevuto diverse proposte di soluzione, molto belle e interessanti, con grafica e illustrazioni chiarissime. Per questo ringraziamo tutti i partecipanti. Di seguito pubblichiamo le nostre proposte di soluzione che a volte sono meno chiare di quelle proposte dal nostri collaboratori utenti.
La croce nel cerchio – soluzioni
1. Una croce con quattro bracci di uguale dimensione è sospesa a una finestra circolare. E’ appesa con tre corde: la corda centrale lunga 25 cm e le altre due sono lunghe 45 cm, come in figura. Il centro della croce e il centro della finestra coincidono. Determinare la misura dei bracci della croce.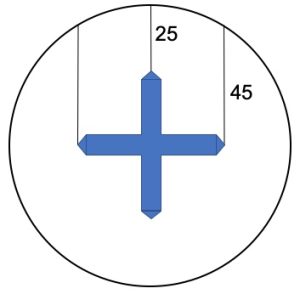
1. SOLUZIONE. Indichiamo con x la lunghezza di un braccio della croce, per cui il raggio del cerchio è 25 + x. Con Pitagora (25 + x)2 – 452 = x2. Svolgendo 625 + x2 + 50x – 452 = x2 che diviene 50x = 1400 da cui x = 28. Un braccio misura 28 cm per cui la larghezza della croce è 28 * 2 = 56 cm.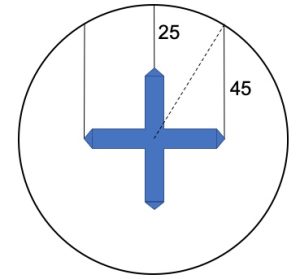
2. Cinque quadrati uguali sono stati disegnati all’interno di una circonferenza di raggio 5 cm, come proposto in figura. Determinare l’area del quadrato rosso.
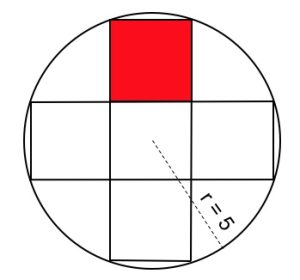
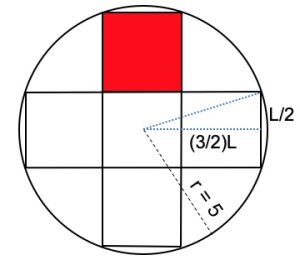
2. SOLUZIONE. Indicando con L il lato di un quadrato, come in figura, con Pitagora avremo: (3L/2)2 + (L/2)2 = 25 svolgendo 9L2/4 + L2/4 = 25 che diviene 10L2 = 100
L = √10 quindi area del quadrato = 10 cm2.
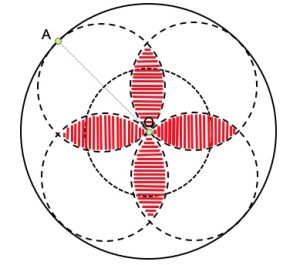
3. Calcolare l’area della croce tratteggiata in rosso, sapendo che il raggio del cerchio OA è 10 cm e i cinque cerchi tratteggiati sono uguali.
3. SOLUZIONE. Consideriamo quarto di cerchio OEL di raggio 5 e il relativo triangolo rettangolo isoscele OEL, evidenziato in blu. La differenza tra l’area del quarto di cerchio e l’area del triangolo è 1/8 della croce tratteggiata in rosso.Area tratteggiata = (25π/4 – 25/2)·8 che diviene [(25π – 50)/4] ·8 = 57 cm2.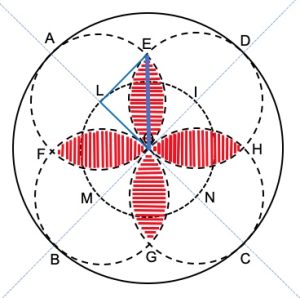
4. Il diametro del cerchio misura 10 cm e i lati della croce, iscritta nel quadrato, sono uguali, come mostrato in figura. Calcolare il perimetro della croce.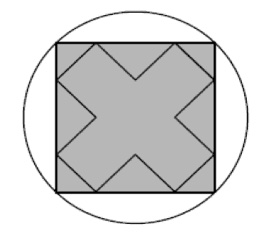
4. SOLUZIONE. Indichiamo con AB il lato del quadrato e CB il diametro del cerchio, come in figura, con Pitagora avremo AB = CB / √2 = 7,07 cm. Il lato del quadrato è diviso in 4 parti uguali e ognuna di queste quattro parti è, a sua volta, il cateto di un triangolino rettangolo isoscele come indicato sul lato AB. Il perimetro della croce è composto da 12 lati uguali e ogni suo lato corrisponde all’ipotenusa del triangolino rettangolo isoscele. Con il teorema di Pitagora, di nuovo, calcoliamo l’ipotenusa ossia il lato della croce √2 · (AB/4) = 2,50 che moltiplicato per 12 dà il perimetro della croce, 30 cm.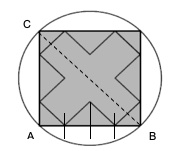
Allo stesso risultato si può arrivare considerando l’ara del quadrato, l’area della croce e l’area residua. L’area del quadrato, che è 50 cm2, si può scomporre in 32 piccoli triangoli rettangoli isosceli uguali, dodici dei quali sono esterni alla croce e venti sono interni alla croce . La croce è composta da cinque quadratini uguali e ogni quadratino è composto da quattro di questi triangolini, perciò:
area di un triangolino 50 / 32 = 1,5625 cm2
area di un quadratino della croce 1,5625 · 4 = 6,25 cm2
lato del quadrato √6,25 = 2,5 cm. Infine perimetro della croce 2,5 · 12 = 30 cm.
I Giochi del Lunedì di Prisma tornano tra due settimane.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).