I Giochi del Lunedì di Prisma del 25 marzo 2024 a cura di Fabio Ciuffoli
Oggi proponiamo quattro problemi che mettono in relazione due simboli antichissimi: la croce e il cerchio. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le soluzioni.
La croce nel cerchio
1. Una croce con quattro bracci di uguale dimensione è sospesa a una finestra circolare. E’ appesa con tre corde: la corda centrale lunga 25 cm e le altre due sono lunghe 45 cm, come in figura. Il centro della croce e il centro della finestra coincidono. Determinare la misura dei bracci della croce.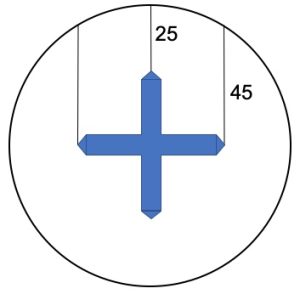
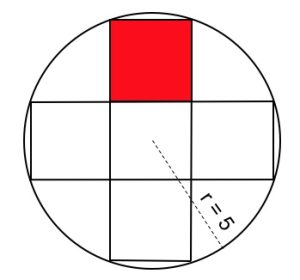
2. Cinque quadrati uguali sono stati disegnati all’interno di una circonferenza di raggio 5 cm, come proposto in figura. Determinare l’area del quadrato rosso.
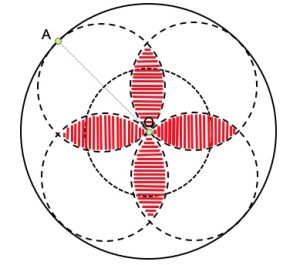
3. Calcolare l’area della croce tratteggiata in rosso, sapendo che il raggio del cerchio OA è 10 cm e i cinque cerchi tratteggiati sono uguali.
4. Il diametro del cerchio misura 10 cm e i lati della croce, iscritta nel quadrato, sono uguali, come mostrato in figura. Calcolare il perimetro della croce.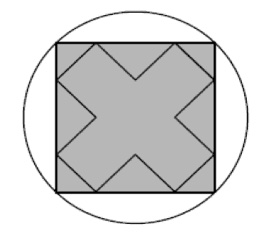
Aggiornamento per le soluzioni click qui.
Il problema n. 3 ha fatto parte delle prova finale dei Giochi Internazionali di Matematica svolti a Parigi nel 2010.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
14 risposte
Con il Teorema delle corde vedi disegno
(25 + b) : 45 = 45 : 25
25 + b = 2.025/25 = 81 da cui b = 81 – 25 = 56.
Problema 1. vedi disegno
Problema 3.
Non ripeto la soluzione, già esposta giustamente da altri.
Esprimo solo un dubbio:
Che senso ha aggiungere che anche il quinto cerchio, quello centrale, è uguale agli altri?
Io non ho usato questo dato per risolvere il problema.
E’ vero non serve. Potrebbe, però, suggerire una modalità di soluzione, che anche io ho utilizzato. A domani per le soluzioni.
Problema 2. Indico con x il lato di un quadrato, applico Pitagora al triangoo rettangolo evidenziato in figura che ha ipotenusa 10 cateto verticale 3x. vedi disegno
Problema 3 vedi allegato
Di seguito la soluzione del problema n° 4
Problema 3.
R = 10 cm.
L = R/2
S = (π-2) × L^2/2 = (π-2) × R^2/8
C = 4×S =( π-2)×R^2/2 = (π-2)×50 cm^2.
2. Vedi disegno
Problema 2. Area del quadrato rosso = 10.
Problema n 1. vedi immagine
N 1. 45 * 45 = 25 * (L+25)
L=56
Problema 1 vedi allegato
1. Detto x la metà lunghezza della croce e AB la corda che unisce i punti di attacco delle corde di 45 cm, col teorema di Euclide nel triangolo rettangolo inscritto nel semicerchio di vertice in B si ha: x^2=(x-20).(x-70) da cui x=28 e 2.x=56 cm.