117. Soluzioni del 26 febbraio 2024 – Il Dilemma del Prigioniero, il Dilemma del Profeta e le strategie di cooperazione motivate da egoismo

Le soluzioni del 26 febbraio 2024 a cura di Fabio Ciuffoli 

Ieri abbiamo presentato quattro problemi sul Dilemma del Prigioniero e sulle strategie collaborative o competitive. Di seguito pubblichiamo le nostre proposte di soluzione e le relative argomentazioni. 

1. Il Dilemma del Prigioniero e la coimprenditorialità turistica – soluzione 

1. Due albergatori, A e B, possono decidere autonomamente tra due forme di utilizzazione dell’ambiente: rispettarlo (R) oppure danneggiarlo (D). Chi sceglierà la strategia del rispetto dell’ambiente dovrà sostenere maggiori costi (depuratori per non inquinare, spazi verdi, parcheggi auto attrezzati, ecc.). Chi sceglierà la strategia del danneggiamento, sfruttando in modo intensivo l’ambiente, non sosterrà costi aggiuntivi e di conseguenza avrà maggiori profitti. Nella tavola seguente sono indicate le quattro combinazioni di strategie, in ogni quadrante sono riportati i profitti in migliaia di euro dei due albergatori concorrenti: in alto a destra il profitto dell’albergatore A in rosso, in basso a sinistra quello dell’albergatore B in blu.

Il quadrante in alto a sinistra (20,20) indica il risultato della scelta di danneggiare sia di B che di A, il profitto di B è 20 e quello di A è 20. Il quadrante in alto a destra (70,10) indica che, se B danneggia l’ambiente mentre A  lo rispetta, i profitti di B sono 70 e quelli di A sono 10 e via di seguito. Ciascun albergatore può comunicare con l’altro, può mentire o essere leale, rispettare i patti oppure trasgredirli, come verosimilmente accade nella realtà.

1. Per ottenere il massimo profitto, quale strategia tra rispetto o danneggiamento dovrà adottare ciascun albergatore?

1. SOLUZIONE. Le strategie scelte saranno D,D, anche se questo risultato non è un ottimo economico: ciascun partecipante cercherà di ottimizzare la propria posizione ma finirà in condizione subottimale. Ad esempio, consideriamo la tavola di decisione di B, colori blu, che è la seguente

Per l’albergatore B, la scelta D è dominante perché permette risultati migliori della scelta R, qualsiasi sia la scelta di A: infatti 20 è maggiore di 10 e 70 è maggiore di 50. E lo stesso vale per l’albergatore A. In conclusione essi sceglieranno D,D non riuscendo a cogliere l’opportunità R,R che permetterebbe maggiori profitti per entrambi.

2. Il Dilemma del Profeta – soluzione 

Supponiamo che questo gioco sia ripetuto molte volte con un guadagno totale pari alla somma di tutti i giochi, come verosimilmente accade nella realtà. Un giocatore potrebbe “profetizzare” il comportamento dell’altro giocatore introducendo un fattore di ponderazione del rischio e ricalcolando i profitti, i giocatori potrebbero stipulare accordi e contratti con clausole punitive per chi non rispetta le regole e via di seguito.

2. Quale strategia adotterebbe l’albergatore B, se pensasse che anche l’albergatore A facesse le sue stesse scelte, supponiamo con un indice di fiducia del 90%?

2. SOLUZIONE. La tavola delle decisioni di B diventerebbe

I Valori Monetari Attesi, ossia profitti ponderati alla percentuale di probabilità, delle strategie di rispetto o di danneggiamento, per l’albergatore B sarebbero:, 

VMA (D) = 20 * 0,9 + 70 * 0,1 = 25 (Valore Monetario Atteso di B con la strategia danneggiamento). 

VMA (R) = 10 * 0,1 + 50 * 0,9 = 46 (Valore Monetario Atteso di B con la strategia rispetto)

perciò la strategia di B, che massimizza il valore monetario atteso, è R. A questo punto il principio di massimizzazione del valore monetari atteso, con un alto indice di fiducia (0,9), consiglia di rispettare l’ambiente. Le strategie dipendono dal grado di fiducia tra i concorrenti: se la fiducia è bassa, prevale il principio conflittuale di dominanza, mentre se la fiducia è alta, allora prevale il principio cooperativo. In questo quadro, gli interventi di Politica Economica possono essere fondamentali per determinare il clima di fiducia tra gli imprenditori!

2.1. Approfondimento. Sapreste calcolare l’indice di fiducia che rende indifferente la scelta dei due albergatori tra danneggiare o rispettare l’ambiente?

2.1. SOLUZIONE. Indicando con x l’indice di fiducia, si imposta la seguente equazione:

VMA (D) = VMA (R)

20*x + 70*(1 – x) = 10*(1 – x) + 50*x  che diviene 

20x + 70 – 70x = 10 – 10x + 50x  

90x = 60 da cui x = 0,66.

L’indice di fiducia che uguaglia i valori monetari attesi è 66%. Questo significa che se l’albergatore  B crede che anche l’albergatore A rispetterà l’ambiente con una fiducia del 66% o superiore, allora B sceglierà la strategia del rispetto. Viceversa se l’indice fosse  inferiore al 66%, allora B sceglierà la strategia del danneggiamento. E lo stesso vale per A. 

3. Strategie di cooperazione motivate da egoismo – soluzione 

Siamo sicuri che la cooperazione sia sempre e in ogni caso la miglior strategia?  Supponiamo di partecipare al seguente gioco (Gioco ideato da Douglas Hofstadter pubblicato su  “Scientic American”). Ad ogni concorrente viene sottoposta la seguente tabella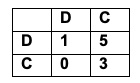I numeri rappresentano importi in dollari. I concorrenti possono essere due o più. Ogni concorrente può scegliere se disertare (D) o cooperare (C). Un ente esterno svolge il ruolo simbolico di “banco” e pagherà i premi ai singoli giocatori. I giocatori saranno premiati in base alle scelte degli altri partecipanti. Se diserti prendi 1$ per ognuno degli altri che diserta e 5$ per ciascuno degli altri che coopera. Se cooperi prendi 0 dollari per ciascuno degli altri che diserta e 3$ per ciascuno degli altri che coopera. Nessun concorrente può perdere in valore assoluto perché non ci sono numeri negativi . Ad esempio con due giocatori: se io diserto e anche l’altro diserta, io guadagno 1$ e l’altro giocatore guadagna 1$; se io diserto e l’altro coopera, io guadagno 5$ e l’altro guadagna zero; se io coopero e l’altro diserta, il mio guadagno è zero e l’altro prende 5$; se io coopero e l’altro coopera, il mio guadagno è 3$ e anche l’altro giocatore prende 3$.

Osservando la tabella, ogni giocatore ha una strategia dominante: disertare. Se diserta guadagna 1$ anziché zero oppure guadagna 5$ anziché 3$ a seconda delle scelte dell’altro.

In questo gioco i disertori fanno diminuire il guadagno medio di tutti i partecipanti, i cooperatori lo fanno salire. Il guadagno medio è dato dal seguente rapporto: tot. esborsi banco/n. partecipanti.

3. Se partecipassero 20 giocatori, quale sarebbe la strategia che permetterebbe il più alto valore del guadano medio?

3. SOLUZIONE. Se partecipassero 20 giocatori e disertassero tutti, ciascuno riceverebbe 19$, così il banco sborserebbe 380$ (19*20) con un guadagno medio di 19$.

Se ci fosse un solo cooperatore e 19 disertori, il cooperatore non riceverebbe nulla, mentre gli altri riceverebbero 1$ per ciascun disertore (18) e 5$ per il cooperatore così il banco sborserebbe 437$ cioè [(18 + 5)*19] che corrisponde a un guadagno medio di 21,85$

Se tutti cooperassero, ciascuno riceverebbe 57$ (19*3) e il banco sborserebbe 1.140$ (20*57) che dà il guadagno medio più alto possibile 57$ e questa è la risposta corretta alla domanda del problema.

Se ci fosse un solo disertore, egli riceverebbe 95$ (19*5) ed il banco pagherebbe 1.121$ (3*18*19 + 95) con un guadagno medio 56,05$.

In sintesi se partecipassero 20 giocatori, la strategia che permetterebbe il più alto valore del guadagno medio sarebbe quella con 20 collaboratori con un guadagno equamente distribuito di 57$ per ciascun giocatore. 

4. Strategie miste – soluzione 

Ora ipotizziamo che i numeri e i segni, riportati in tabella, cambino e diventino quelli proposti di seguito.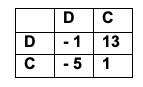

In questo caso vi sono numeri negativi, ciò vuol dire che i giocatori possono anche perdere e quindi pagare una somma al banco.  Ad esempio se tutti i venti partecipanti cooperassero, il banco sborserebbe 19$ e se tutti disertassero, incasserebbe 19$.

4. Quale strategia permette il maggior valore del guadagno medio? E come è possibile assegnare equamente i guadagni tra i partecipanti?

4. SOLUZIONE. Sviluppando i calcoli, consideriamo la seguente tabella riferita a un numero di cooperatori da 10 a 18.

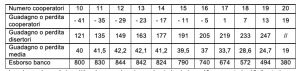
La prima colonna è descrittiva, la seconda colonna riporta i valori con 10 cooperatori e 10 disertori, la terza colonna riporta i valori con 11 cooperatori e 9 disertori, la quarta colonna con 12 cooperatori e 8 disertori e via di seguito.  Illustriamo come si ottengono i valori della seconda colonna, con 10 cooperatori e 10 disertori: ogni cooperatore incassa 9$ per i 9 cooperatori e paga 50$ per i 10 disertori, quindi perde 41$; ogni disertore incassa 130$ per i 10 cooperatori e paga 9$ per i 9 disertori, quindi guadagna 121$. Il “banco” paga 1.210$ e incassa 410$ quindi esborsa 800$ per un guadagno medio a partecipante di 40$ (800/20) distribuito in modo molto iniquo. 

Il gruppo composto da 12 cooperatori ed 8 disertori rende massimo il guadagno medio del gruppo e quindi l’esborso totale del banco che è 844$, ma il gioco è molto iniquo perché i cooperatori perdono 29$ e i disertori guadagnano 149$. Per assegnare equamente l’esborso del banco tra i partecipanti si può utilizzare una strategia mista basata sulle probabilità, per esempio mettendo 12 palle bianche e 8 nere in un’urna e ogni volta che si gioca si estrae una palla a caso: se bianca si coopera, se nere si diserta. L’analisi matematica mostra che se tutti i giocatori seguono questa strategia probabilistica, in media tutti avranno un guadagno di 42,2 $ (844 : 20 = 42,20).  In questo caso la strategia migliore, al fine di ottimizzare il sistema, non è la cooperazione ma quella di decidere su base probabilistica, di volta in volta, se cooperare o disertare. Questo semplice caso dimostra che non basta essere ingenuamente animati da buona volontà. Se le situazioni sono complesse può essere necessario usare strategie miste determinate in base a valori di probabilità. In casi come questi, l’appellativo “cooperatore” cambia significato, sarà più corretto chiamare “cooperatore” chi adotta la strategia basata sul calcolo delle probabilità.

In sintesi la strategia che permette il maggior valore del guadagno medio è 12 cooperatori e 8 disertori. Per assegnare equamente i guadagni tra i partecipanti si può ricorrere a strategie miste basate sulle probabilità.  

I Giochi del Lunedì di Prisma tornano tra due settimane.