
Giochi del Lunedì di Prima del 12 febbraio 2024 a cura di Fabio Ciuffoli
Nel mondo della matematica ricreativa, il sito Mathigon https://mathigon.org propone un’ottima selezione di enigmi e giochi matematici. È un sito web gratuito, ottimo per studenti, insegnanti e semplici appassionati. La maggior parte dei problemi è semplice da comprendere, ma le soluzioni richiedono un procedimento creativo e non convenzionale. Di seguito presentiamo sei problemi tratti da questo sito e invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le nostre soluzioni.
Mathigon: il parco giochi matematico
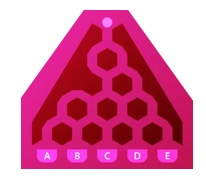
1. Con un solo taglio in linea retta dividere la forma di colore chiaro, disegnata nella figura seguente, in due pezzi per formare un quadrato.

3. Quale proporzione occupa l’acqua nella bottiglia in figura?4. Qual è il rapporto tra le aree del triangolo e la “falce di luna”, disegnata in roso scuro, formata da due archi circolari?
5. Qual è l'area del semicerchio scuro collocato simmetricamente all'interno di un quarto di cerchio nella figura seguente?
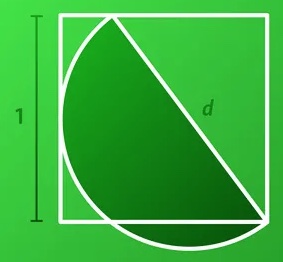
6. Un semicerchio è disposto all’interno un quadrato di lato 1 come proposto in figura seguente. Qual è il diametro del semicerchio?
Aggiornamento per le soluzioni click qui.
I problemi sono tratti dal sito web Mathigon.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
13 risposte
Problema n° 4. Siamo nel caso della lunula di Ippocrate di Chio (che nel V secolo a.c. studiò e dimostrò questo problema).
Lo stesso matematico dimostrò che sottraendo al semicerchio costruito sull’ipotenusa di un triangolo rettangolo isoscele, il settore circolare di centro A e raggio il cateto del triangolo r. isoscele stesso, si ottiene la cosiddetta “lunula di Ippocrate”, che ha area uguale a quella del suddetto ∆.
Dunque il rapporto tra l’area della falce di luna (lunula) e l’area del triangolo r. isoscele è uguale a 1.
2) (1/2)^3+(1/2)^4=3/16
4) preso pari a 2 il cateti del triangolo, l’area del triangolo è 2, quella del settore circolare con centro nel vertice retto è π, quindi l’area del segmento circolare è π-2.
L’ipotenusa è lunga 2√2 quindi la semicirconferenza ha raggio √2 e area π. La lunula ha quindi area π-(π-2)=2. Quindi il rapporto è 1.
5) sia r il raggio del semicerchio. Tracciamo i due raggi che collegano il centro del semicerchio con i punti A e B di tangenza sui raggi del quarto di cerchio, formando il quadrato OABC. La diagonale del quadrato, OC, ha lunghezza √2r.
Disegnamo il raggio del quarto di cerchio per connettere OE e consideriamo il triangolo rettabgolo OCE, da cui possiamo scrivere l’equazione (√2r)^2+r^2=1 che risolra dà r=√3/3
Quindi, l’area del cerchio diventa π/6
Problema 6. Vedi immagine allegata
Problema 5. Vedi immagine allegata
L’area del Triangolo e l’area della Falce di luna sono uguali.
Si può notare infatti che sono entrambi complementari del segmento circolare che si trova in mezzo a loro.
Le aree del quarto di cerchio con centro nel vertice in basso a sx e del semicerchio con centro sul lato obliquo del triangolo sono uguali, facilmente calcolabili pari a (Pi/4)*r^2, ove r è il lato del triangolo.
Problema 2.
in B probabilità è 18,75%
Ho pensato di lanciare 16 palline e di contare semplicemente quante entrano (sommandosi) ed escono (dimezzandosi) da ogni tratto verticale.
Nel contenitore B andranno:
(16/2+16/2/2)/2/2=3
Per completezza, in ogni contenitore finiranno:
A. 0 palline (0%)
B. 3 p (18,75%)
C. 7 p (43,75%)
D. 5 p (31,25%)
E. 1 p (6,25%)
Perfetto e completo
Problema 1.
[immagine allegata]
Problema 6 allego immagine
Problema della bottiglia. Questo tipo di problema presenta la difficoltà che non e’ possibile evincere il volume totale (e quindi la capacità) del recipiente avendo questo sezione variabile.
Tuttavia e’ possibile osservare che in entrambi i casi il livello dell’acqua capita ad un’altezza alla quale la sezione e’ costante. Dal riquadro di destra si vede che la capacita’ del “vuoto” rimanente (pari al volume di liquido che dovrei versare per riempire completamente la bottiglia) e’ pari ad un cilindro di altezza pari a 5 (parlo di cilindro proprio perche’ siamo nella parte a sezione costante).
Quindi, a sinistra, la bottiglia si riempirebbe se al “cilindro pieno” di altezza pari a 10 versassi l’acqua di un cilindro di pari sezione ed altezza 5.
Se ne deduce che la capacità complessiva del recipiente e’ equivalente a quella di un cilindro avente la stessa sezione del fondo della bottiglia ed altezza 15. Tale cilindro sarebbe pieno per una frazione pari a 10/15 = 2/3.
Quesito 3. 20 – 15 = 5
Proporzione 10 : 5 = x : y
y = x/2
x + y = 1
x + (x/2) = 1
x = 2/3
y = 1/3
Nella bottiglia l’acqua occupa i 2/3. vedi immagine
Tutto sta nell’ osservare che la parte occupata dall’ acqua a sinistra è un cilindro alto 10 mentre la parte vuota a destra è un cilindro alto 5, perciò il vuoto è la metà del pieno.
Problema 6. Vedi disegno