112. Soluzioni del 18 dicembre 2023 – Giochi logici da tavolo

Soluzioni del 18 dicembre 2023 a cura di Fabio Ciuffoli

Ieri abbiamo presentato quattro giochi logici da tavolo e di seguito pubblichiamo le soluzioni. 

Giochi logici da tavolo – soluzioni 

1. Strategia e punteggio vincente. Aldo e Bruno si sfidano. Vince chi riesce ad ottenere la somma maggiore dei numeri di dieci carte con valori dallo 0 al 9. Bruno dispone le carte in fila orizzontale nell’ordine che ritiene più opportuno. Ad esempio nel modo seguente:

A turno, ognuno dei due contendenti deve togliere una sola carta da una delle due estremità della fila. Vince chi alla fine ha ottenuto il totale più alto sommando i valori delle cinque carte. Il pareggio è impossibile perché la somma dei valori in gioco è 45 che è dispari. La prima mossa spetta ad Aldo, per bilanciare il vantaggio concesso a Bruno nel disporre le carte. Esiste una strategia vincente che consente a uno dei due giocatori di vincere sempre? E’ possibile prevedere in anticipo il punteggio?

1. SOLUZIONE. Esiste una strategia vincente per Aldo che sarà anche in grado di prevedere il punteggio finale. Aldo deve sommare i valori delle carte di posto dispari e quelle di posto pari, valutando quale delle due è più alta. Nell’esempio precedente la somma più alta corrisponde ai valori delle carte di posto dispari, con un totale di 24, mentre i valori delle carte di posto pari sommano 21. Aldo deve riuscire a prendere tutte le carte che si trovano nelle posizioni dispari, forzando l’avversario a prendere le altre.  Aldo vincerà 24 a 21. Generalizzando: se la somma più alta fosse data dalle carte dispari, allora Aldo dovrà iniziare a prendere la carta che si trova nell’estremità sinistra, di posto dispari nel nostro esempio la carta 3; se la somma più alta fosse data dalle carte dispari, allora dovrà prendere quella che si trova all’estremità destra, nel nostro esempio la carta 7. Successivamente ad Aldo conviene prelevare ogni volta la carta che si trova nella posizione attigua a quella che ha preso il suo avversario.

2. I dieci fiammiferi: vince chi preleva l’ultimo. Dopo aver allineato 10 fiammiferi sul tavolo Carlo propone a Dario un gioco che consiste nel prelevare a turno uno, oppure due, o anche tre fiammiferi. Vince chi preleva l’ultimo. Carlo gioca per primo: quanti fiammiferi deve prendere, in questa sua prima mossa, per essere sicuro di vincere?

2. SOLUZIONE. Carlo può essere sicuro di vincere e deve prendere due fiammiferi. Per la dimostrazione, conviene procedere a ritroso, partendo dall’ultima mossa. Per essere sicuro di vincere, Carlo deve fare in modo che alla penultima mossa a Dario restino esattamente 4 fiammiferi e che, alla mossa precedente, ne restino 8. Pertanto alla prima mossa Carlo ne deve prelevare 2.

3. Fissare un numero. Si fissa un numero come somma finale, ad esempio 30. Due giocatori, Giacomo e Ivano, in questo ordine a turno scelgono un numero da 1 a 6 e lo sommano al risultato precedente. Vince chi arriva per primo al numero prefissato, 30, senza oltrepassarlo.

• E’ conveniente essere il primo giocatore, Giacomo oppure il secondo giocatore, Ivano?
• E se il numero prefissato, anziché 30, fosse scelto dal secondo giocatore, Ivano, quale strategia potrebbe scegliere per vincere?

3. SOLUZIONE. Chi gioca per primo, Giacomo, deve seguire la seguente scala di numeri 2, 9, 16, 23. Infatti se Giacomo gioca  2, Ivano al massimo può arrivare a 8 ed al minimo a 3. Quindi Giacomo, aggiungendo opportunamente un numero da 1 a 6, può arrivare sempre a 9. Ivano al minimo arriva a 10 e al massimo a 15, quindi Giacomo può arrivare a 16.
Ivano al minimo arriva a 17 e al massimo 22, perciò Giacomo può sempre arrivare a 23. Ivano arriva al minimo a 24 e la massimo a 29 e quindi Giacomo arriva per primo a 30.

In generale, sia s la somma da raggiungere e n il numero massimo che può essere aggiunto: si divide s per n+1. Il resto è il primo numero della scala. Gli altri numeri si ottengono sommando, al primo, n+1.
Ad esempio se  s = 30 ed n = 6 avremo 30/7 = 4 e resto 2. Quindi 2 sarà il primo numero della scala. Gli altri numeri saranno 2 + 7 = 9; 9 + 7 = 16; 16 + 7 = 23.
Un altro esempio con s = 40 e n = 6 avremo 40/7 = 5 e resto 5. Quindi 5 sarà il primo numero della scala. Gli altri numeri saranno 12, 19, 26, 33.

Se il resto della divisione fosse zero, ad esempio con s = 35 ed n = 6 quindi 35/7 = 5 con resto zero, allora il secondo giocatore, Ivano, avrà una strategia vincente, seguendo la scala: 7, 14, 21, 28, 35. Ivano, per vincere, deve fissare un numero, s, che sia multiplo di n+1, nel nostro caso un multiplo di 7.

4. Il 15 vince. Due giocatori, Enrico e Flavio, a turno prendono una qualsiasi delle nove carte numerate progressivamente da 1 a 9, come in figura seguente. Vince chi per primo raggiunge il valore 15 sommando tre delle sue carte, non necessariamente le prime. Inizia Enrico. Quale tessera dovrà prendere Flavio nella sua prima mossa per cercare di non perdere?

4. SOLUZIONE. Il gioco si può schematizzare utilizzando la seguente tabella 3×3 che riporta tutte le terne x, y, z di numeri interi compresi tra 1 e 9 per cui x + y + z = 15. 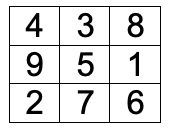Si tratta di un quadrato magico con costante magica uguale a 15. Se il primo giocatore, Enrico, scegliesse un numero pari, ossia uno posto ai vertici del quadrato, per il secondo giocatore,  Flavio, sarà sufficiente scegliere il 5. Il primo giocatore dovrà successivamente muoversi in orizzontale o in verticale e il secondo potrà sempre neutralizzarlo, come nel noto gioco del tris. Analoga situazione se il primo giocatore scegliesse un numero dispari diverso da 5. Se invece il primo giocatore scegliesse il 5, per il secondo sarà sufficiente scegliere un numero pari. Il primo giocatore si dovrà poi muovere in orizzontale, in verticale o lungo una delle due diagonali e il secondo avrà sempre la possibilità di neutralizzarlo.

I giochi prendono spunto dai libri dell’amico Ennio Peres (1945 – 2022).