
Soluzioni del Giochi del 20 novembre 2023 a cura di Fabio Ciuffoli
Ieri abbiamo presentato quattro giochi che hanno fatto parte del World Math Contest, organizzato dal nostro Centro PRISTEM dell’Università Bocconi e svolto on line a livello mondiale il 24 settembre 2022. Di seguito pubblichiamo le varie proposte di soluzione.
World Math Contest
1. I geyser matematici. Nel parco di Yellowstone due geyser emettono vapore in modo molto regolare: il primo esattamente ogni 24 minuti, il secondo ogni 9 minuti. Ieri, alle 20:22, entrambi i geyser hanno emesso un getto di vapore. A che ora, per la prima volta dopo le 20:22, è successo di nuovo?
1. SOLUZIONE. Troviamo il minimo comune multiplo dei numeri 24 e 9, ossia è 72. Ora sommiamo i 72 minuti (1 ora e 12 minuti) alle ore 20:22 e otteniamo ore 21:34 che è l’orario in cui entrambi i geyser emetteranno un getto di vapore.
2. Crittografia multilingue. Risolvi il seguente criptaritmo, sostituendo ogni lettera con una cifra compresa tra 1 e 9, alla stessa lettera corrisponde la stessa cifra e lettere diverse indicano cifre diverse. Il carattere sulla seconda riga è la cifra “0”.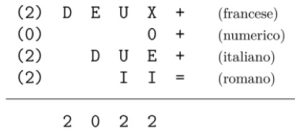
A quale numero corrisponde la sequenza IDEE?
2. SOLUZIONE. Iniziamo osservando che il valore del riporto delle centinaia (E + D) non può essere diverso da 1 e di conseguenza D deve essere 1. Lasciamo al lettore impostare le varie ipotesi e le relative verifiche. Il numero della sequenza IDEE è 3177, inoltre U = 9 e X = 2.
3. Il pesce controcorrente. Bob, utilizzando 13 monete uguali, ha ottenuto un pesciolino (a sinistra in figura), ma si accorge che sta nuotando contro-corrente. Alice, spostando alcune monete del pesce di Bob, ottiene lo stesso pesciolino (a destra in figura), ma che nuota nella direzione opposta.
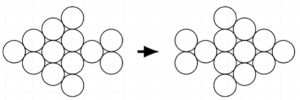
Qual è il numero minimo di monete che Alice deve spostare per ottenere il suo pesciolino?
3. SOLUZIONE. Consideriamo la simmetria attorno alla colonna che contiene quattro monete. Il numero minimo di spostamenti è 3, come illustrato in figura.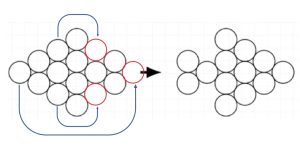
4. Quadrati nel triangolo. Il triangolo isoscele in figura è diviso a metà dell’altezza, che misura i 2/3 della base. Il quadrato inclinato, a sinistra, ha il lato di 35 mm. Quanto misura, in mm, il lato del quadrato di destra?

4. SOLUZIONE. Presentiamo tre diversi metodi per la soluzione.
4.1 – Triangoli simili. Indichiamo con b la base, con h l’altezza e con L il lato del triangolo isoscele e con L1 e L2le relative misure parziali e con x il lato del quadrato sulla destra, come in figura seguente.
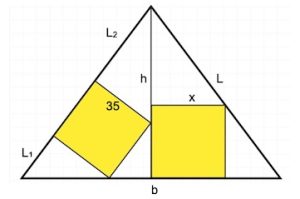
Sappiamo che h = (2/3)b. Con Pitagora determiniamo L = √[(4/9)b² + b²/4] = √(25/36)b² = (5/6)b.
Triangoli simili b/2 : (2/3)b = L1 : 35
L1 = (b/2)•35/(2/3)b = 105/4 mm;
Triangoli simili (b/2) : ( 2/3)b = 35 : L2
L2 = (2/3)b•35/(b/2) = 140/3 mm;
L = 105/4 + 35 + 140/3 = (315+420+560)/12 = 1295/12 mm;
b = (6/5)L = 259/2 mm;
h = (2/3)b = 259/3 mm;
Triangoli simili (b/2) : (2/3)b = x : (h-x)
(b/2) : (7/6)b = x : h
x = [(b/2)h] / [(7/6)b] = (3/7)h = 259/7 = 37 mm
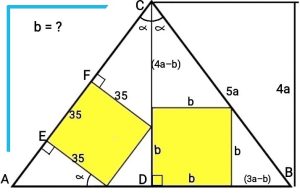
4.2 – Teorema del quadrato inscritto in un triangolo. Proposta da Carmelo Giugno con disegno autografo.
Definiamo: 2a il valore della base del triangolo equilatero, h l’altezza sulla base AC del triangolo rettangolo ACD, l il lato del quadrato di 35 mm e x il lato del quadrato sulla destra.
L’area del triangolo rettangolo ADC = DCB = (5a/3) • (h/2) = (a/2) • (4a/3) da cui h = 4a/5.
Teorema del quadrato inscritto in un triangolo l = [(5a/3) • (4a/5)] / [(5a/3) + (4a/5)] = (4a2/3) / (37a/15) = 35 mm. da cui ricavo a = 259/4.
Teorema del quadrato inscritto in un rettangolo x = (a • 4a/3) / (a + 4a/3) = 4a/7 = (4/7) • (259/4) = 37 mm.

4.3. Trigonometria. Proposto da Massimo Molinelli.

Infine segnaliamo una proposta di soluzione di Alessandro Mazzariol estremamente sintetica.
(5/3+4/5) = 37/15 poi 37/15*35*3/7 = 37 mm.
I Giochi del Lunedì tornando tra due settimane.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).