Menu
I Giochi Lunedì di Prisma del 23 ottobre 2023 a cura di Fabio Ciuffoli
I tre giochi, che presentiamo di seguito, hanno fanno parte delle sfide matematiche settimanali per ragazzi di età dai 13 a 16 anni proposti durante l’anno scolastico alla King’s Maths School di Londra. La scuola si rivolge a studenti con una particolare passione per la matematica, per ogni posto disponibile fanno domanda più di dieci studenti. La scuola utilizza i dottorandi del King’s College in qualità di mentori per gli studenti, fornisce inoltre programmi di aggiornamento e approfondimento professionale per insegnanti di matematica e fisica in altre scuole e ogni settimana pubblica una sfida matematica allo scopo di stimolare curiosità e interesse dei ragazzi. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le soluzioni.
Sfide matematiche alla King’s Math School
1. Sfere e cubi. Un cubo verde si trova all’interno di una sfera blu che tocca gli otto angoli del cubo. La sfera, a sua volta, si trova in un cubo giallo arancione che tocca i bordi della sfera, come disegnato in figura. Quante volte è maggiore il volume del cubo più grande, rispetto al volume del cubo più piccolo?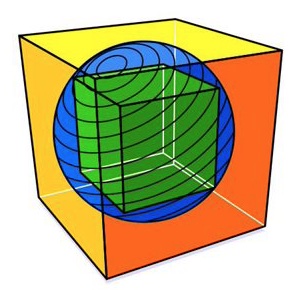
2. Due scale. Il disegno seguente mostra due scale, posizionate tra due pareti, in modo che una scala raggiunga a metri sul muro di sinistra e l’altra scala raggiunga b metri sulla parete destra.
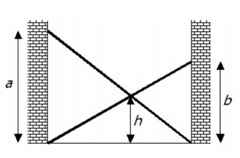Le due scale si incrociano ad un’altezza di h metri dal suolo. È possibile determinare h solo in termini di a e b, oppure abbiamo bisogno di conoscere altre misure, come la lunghezza tra i muri o la lunghezza delle scale?
3. La Torre Eiffel. A Parigi è una bellissima giornata limpida e ti trovi in cima alla Torre Eiffel. Quanto lontano puoi vedere? Più precisamente quanto dista, dalla parte inferiore della torre, il punto più lontano che puoi vedere sulla superficie della Terra? [Sappiamo che: l’altezza della Torre Eiffel è 301 m; il raggio della Terra è circa 6.371 km; si ipotizzano condizioni ideali, sfericità della Terra, visibilità, ecc.]
Aggiornamento per le soluzioni click qui.
I problemi sono tratti e rielaborati dal sito della King’s Math School https://www.kingsmathsschool.com
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
15 risposte
Generalizzazione problema Due Scale. Vedi immagine allegata.
Problema n. 3. Vedi immagine
Problema 2. È possibile determinare h solo in funzione di a e b.
Risulta, dopo facili calcoli, h = ab/(a+b)
1 – Il lato del cubo grande è uguale alla diagonale del cubo piccolo.
Detto x il lato del cubo piccolo, d la diagonale della sua base e
D la sua diagonale abbiamo:
D^2 = x^2 + d^2 = x^2 + 2* x^2 = 3 * x^2
quindi il volume V del cubo grande è:
V = D^3 = (3*x^2) ^ (3/2) = sqrt(27) * x^3
V = sqrt(27) * v , dove v=x^3 è il volume del cubo piccolo.
Vedi immagine allegata
Problema 1 – Senza fare il calcolo completo si può partire dal fatto che la diagonale del cubo verde è uguale al diametro della sfera blu, a sua volta uguale al lato del cubo giallo-arancione.
E dunque il lato del cubo verde equivale al lato del cubo giallo-arancio diviso radice di 3.
Il rapporto tra i volumi di due solidi simili (in questo caso i due cubi) è pari al cubo del rapporto tra le misure lineari, dunque in questo caso è pari al cubo della radice di 3, ovvero 3 x sqrt(3).
Quesito 1) Il rapporto è 8
Quesito 2) h = a*b/(a + b) quindi h dipende solo da a e b e non dalla distanza dei muri.
Quesito 3) se misuriamo la distanza in linea d’aria dalla torre al punto più lontano visibile questa distanza è 61,93086953 Km
Problema n° 1:
R (cubo g./cubo p.) = √27 = 3•√3.✔️
Problema 1. √(27) = 3√3 = 5,196
3. acos(R/(R+h))*R = ~61.929 metri
Perfetto.
1. Rapporto cubo interno sfera 1/2 radq.3 e rapporto cubo esterno cubo interno 3radq3.
Problema 1. 3✓3
La Torre Eiffel: Sfruttando il fatto che l’altezza della torre è molto più piccola del raggio terrestre, tale distanza può essere calcolata, praticamente in modo indifferente, come quella del cateto corto o come quella dell’altezza relativa all’ipotenusa di un triangolo rettangolo che ha per cateto il raggio terrestre e per ipotenusa la somma del raggio terrestre e l’altezza della torre Eiffel.
Se proprio si vuole essere pignoli, da quel trifolo rettangolo si calcola, fon la trigonometria, l’angolo al centro della sfera terrestre e poi si usa questo angolo per calcolare la lunghezza dell’arco
Sfere e cubi: Il cubo interno ha per diagonale lo spigolo del cubo esterno. La diagonale del cubo è radq(3) volte lo spigolo, quindi il cubo esterno ha volume 3radq(3) volte il volume del cubo interno
Due scale: Se la distanza tra i muri aumenta, tenendo fissi a e b (quindi si allungano anche le scale, anche se non in proporzione), si applica alla figura una dilatazione orizzontale, trasformazione geometrica che non modifica le lunghezze verticali, quindi l’altezza dell’intersezione resta la stessa.
Usando le proporzioni deve risultare a/L=h/d, b/L=h/(L-d). Da cui si ricava h=ab/(a+b)