
I Giochi del Lunedì di Prisma del 28 agosto 2023 a cura di Fabio Ciuffoli
Oggi proponiamo tre giochi matematici sulle serie numeriche. Si è discusso molto sulla validità di queste prove nei concorsi e nelle selezioni, infatti in molti casi ci può essere più di una chiave di lettura e quindi i risultati sono opinabili, anche se ciò non toglie nulla al piacere e all’eleganza delle soluzioni che verranno proposte. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le nostre proposte di soluzione.
Serie numeriche
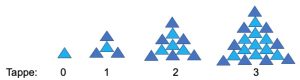
1. Un mosaicista sta realizzando una pavimentazione con una serie di triangoli equilateri tutti uguali tra loro. All’inizio aveva incollato un solo triangolo sul pavimento (tappa 0). In seguito, per ciascun vertice libero della figura della tappa precedente incolla un nuovo triangolo con lo stesso orientamento per il quale il punto medio di un lato coincide con il vertice libero, come illustrato in figura. Quanti triangoli avrà incollato sul pavimento dopo la ventiduesima tappa?
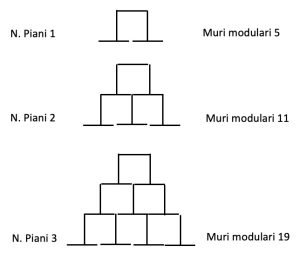
2. Con alcuni muri modulari vengono realizzate le seguenti strutture illustrate in figura: con 5 muri si costruisce un piano, con 11 muri si costruiscono due piani, con 19 muri si costruiscono 3 piani e via di seguito. Quanti piani si costruiranno con 40.601 muri?
3. Il Modulo 1 è composto da 3 quadratini, il Modulo 2 è composto da 10 quadratini e il Modulo 3 è composto da 21 quadratini, disposti come in figura.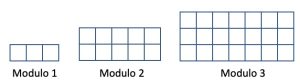
Il primo gioco ha fatto parte del “Tour Giochistico” di Prisma 2022. Il secondo gioco è stato proposto da Carmelo Giugno, che ringrazio per la disponibilità, in un social media di divulgazione matematica. Il terzo gioco è tratto da una prova di accesso all’Università.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
18 risposte
4. Se evinco bene, dato che il numero di quadratini per ogni modulo n è pari al doppio del numero del modulo + 1, allora il modulo 4 conterrà (4*9) quadratini, cioè 36 quadratini.
Il modulo più grande realizzabile con 1235 quadratini sarebbe, dunque, il modulo 24, cioè (24*49) quadratini, cioè 1176. E ne resterebbero 59.
Prob. 1.
Considerando nel conteggio il “soffitto” del piano n come il “pavimento” del piano (n+1), ed escludendo l’elemento di copertura, si ha:
Np=1 Elementi orizzontali 2. Elementi verticali 2
Np=2 O=2+3 V=2+3
Np=3 O=2+3+4
V=2+3+4
.
Np=x
O = V = 2+3+…+(n+1)
(n numero di elementi)
2 (n+3)n/2 + 1 = 40601
n^2 + 3n – 40600 = 0
n1 = 200 soluzione accettabile
n2 = -203
N. 4.
Mod.1 3•1=3
Mod.2 (3+2)•2=10
Mod.3 (3+2•2)•3=21
Mod.4 (3+2•3)•4=36
Mod. n: [3+2•(n-1)]•n=(3+2n-2)n= (2n+1)n
Mod.9: (2•9+1)•9=171 quadratini;
(Mod. n)<=1235 → (2n+1)n<=1235;
2n²+n-1235=0 → n≃24,6
Mod.24: (2•24+1)24=49•24=1176 quadratini
1 Alla tappa n corrispondono 1+3(n+1)n/2 triangoli, per cui n=22 comporta 760 triangoli
2 Al piano n corrispondono (n+2)(n+1)-1 muri, per cui 40601 muri producono 200 piani
3 Al modulo n corrispondono n(2n+1) quadratini, per cui il modulo 9 richiede 171 quadratini e con 1235 quadratini si può ottenere al massimo il modulo 24
Ottimo. A domani per le soluzioni commentate.
Prob n. 3. m_i = 2i × (2i+1) / 2= i(2i+1)
m_4=4×9=36
m_9=9×(18+1)=171
i_max=24
Problema 3. Indicando con N il modulo, il numero dei quadratini dell’N-esimo modulo è: 2N^2 + N. Dunque il quarto midulo ha 36 quadratini; il nono ne ha 171. Con 1235 quadratini si può costruire il modulo massimo con N = 24
problema 1.
per n=0 t(n)=1
per n=1 t(n)=t(n-1)+3
per n=2 t(n)=t(n-1)+6
per n=3 t(n)=t(n-1)+9
per n=4 t(n)=t(n-1)+12
quindi t(n)=1+3Sum[k=1..n]=1+3n(n+1)/2
t(22)=1+3*11*23=760
N. 2 vedi allegato
2) n + (n+1)^2 = 40601
n = 200
A domani pomeriggio per le soluzioni commentate.
Problema 2 – I muri (esclusa la base) sono:
1) 3 = 4-1 = (1+1)^2 – 1
2) 8 = 9-1 = (2+1)^2 – 1
3) 15 = 16-1 = (3+1)^2 – 1
…
n) (n+1)^2 – 1
Quelli della base sono, invece, n+1
In totale avremo:
(n+1)^2 – 1 + n +1 = (n+1)^2 + n = 40601
Da cui, risolvendo, avremo:
n1 = -203 (da scartare)
n2 = 200 piani che si possono costruire con 40601 muri
Problema 1. Vedi allegato
1. 760
2. 6767
3.1 Griglia 4×9
3.2 171
3.3 24
Ottimi 1 e 3. Sul 2 ti chiedo gentilmente il procedimento. A domani per le soluzioni commentate.
Sì scusa. Errore di distrazione ;). Curioso che anche l’approccio sbagliato arrivasse giusto giusto a 40601. 😀
Versione corretta: 200 piani. Ad ogni piano si aggiungono 2 muri in più rispetto a quelli aggiunti precedentemente.
Ottimo a domani per le soluzioni.
1. Ad ogni tappa i si aggiungono 3i triangoli. Tenendo conto che alla tappa 0 è stato posato 1 triangolo, alla tappa generica n saranno stati posati 1 + 3×1 + 3×2 + ….. + 3x i triangoli, quindi 1 + 3x(1 + 2 + 3 + … + n) triangoli. La somma dei primi n numeri naturali è data da nx(n+1)/2, per cui il numero di triangoli alla generica tappa n è dato da 1 + 3n x (n+1)/2.
Per n = 22 si ottiene 1 + (3 x 22 × 23)/2 = 760